2. Spatial Grid

Intro

Для того чтобы уменьшить количество проверок коллизий, можно использовать попробовать реализовать простую идею – нам нет смысла проверять объекты, которые находятся далеко друг от друга.

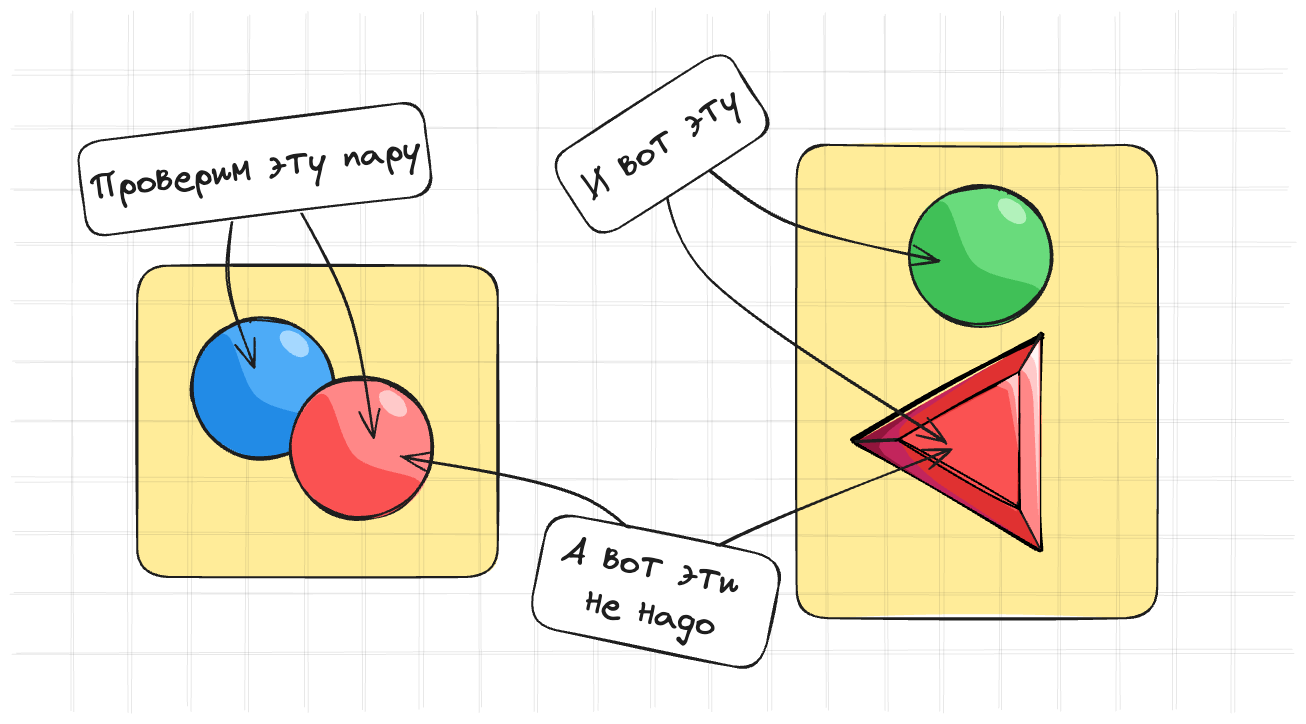
Первая идея которую можно попробовать – выделить большие квадраты и с каждым кадратом можно ассоциировать объекты. Если нам известен максимальный радиус окружающей сферы объекта, то мы можем разбить пространство на квадраты размером в 2 раза больше максимального радиуса окружности. Если все симулируемые объекты примерно одного размера, то такой подход будет работать.

Если же размеры очень отличаются, то получится, что много объектов будут находиться в одном квадрате вот как-то так:

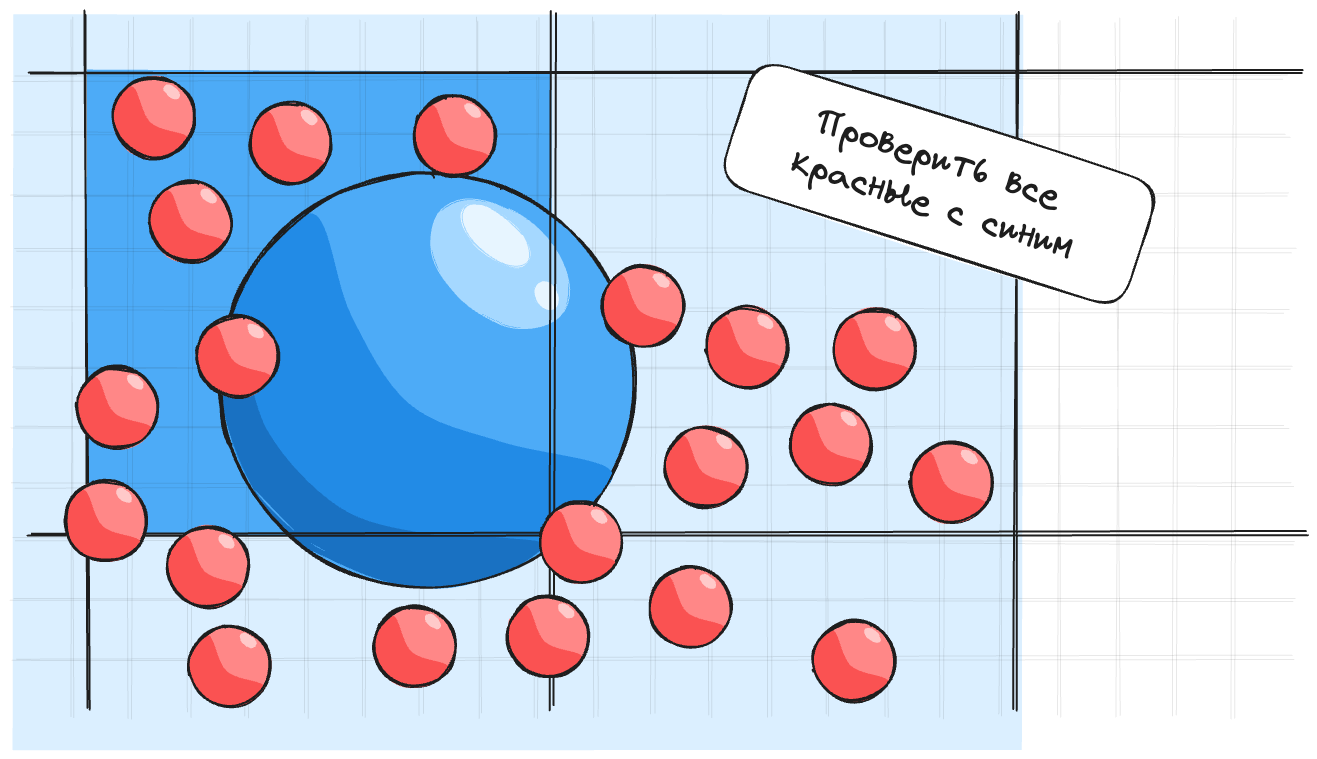
Как хранить объекты

Есть два способа

1. Хранить центр объекта в одном квадрате

Мы назначаем каждому объекту квадрат, в котором находится центр объекта. Чаще всего делают так:

Выбираем размер квадрата cell_size
Для каждого объекта находим квадрат, в котором он находится

    X = floor(x / cell_size)
    Y = floor(y / cell_size)

Для каждого квадрата храним список объектов, которые находятся в нем

Тогда нужно проверить все объекты в квадратах, которые находятся рядом с квадратом объекта. Для 2d нам нужно проверить 9 квадратов (только при условии, что размер ячейки больше диаметра самого большого объекта).

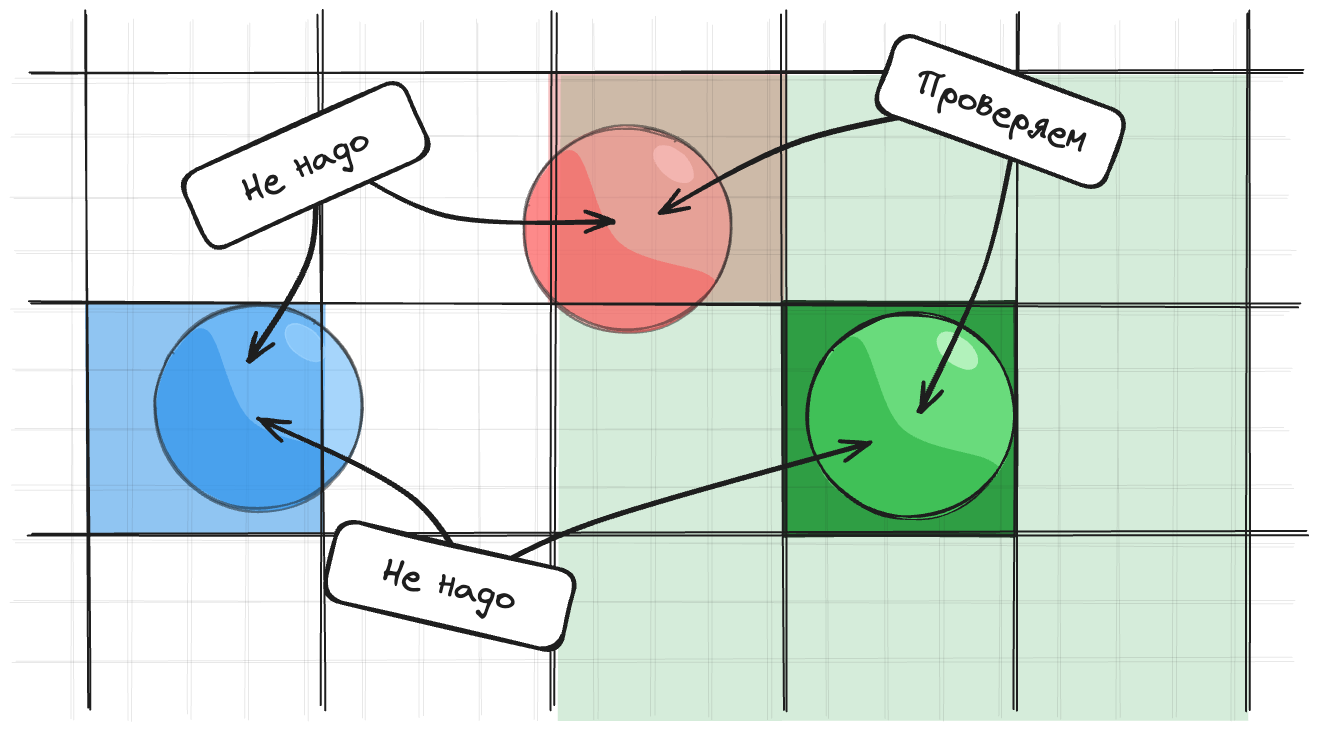
2. Хранить объект в нескольких квадратах

Мы в каждом квадрате храним объекты, которые с ним пересекаются. Т.е в нескольких квадратах будет находиться один и тот же объект.

Для каждого объекта нужно проверить все квадраты, в которых он находится.

Чтобы найти квадраты, в которых находится объект, нужно найти квадраты, которые пересекаются с объектом.

    X1 = floor((x - r) / cell_size)
    Y1 = floor((y - r) / cell_size)
    X2 = floor((x - r) / cell_size)
    Y2 = floor((y + r) / cell_size)
    X3 = floor((x + r) / cell_size)
    Y3 = floor((y - r) / cell_size)
    X4 = floor((x + r) / cell_size)
    Y4 = floor((y + r) / cell_size)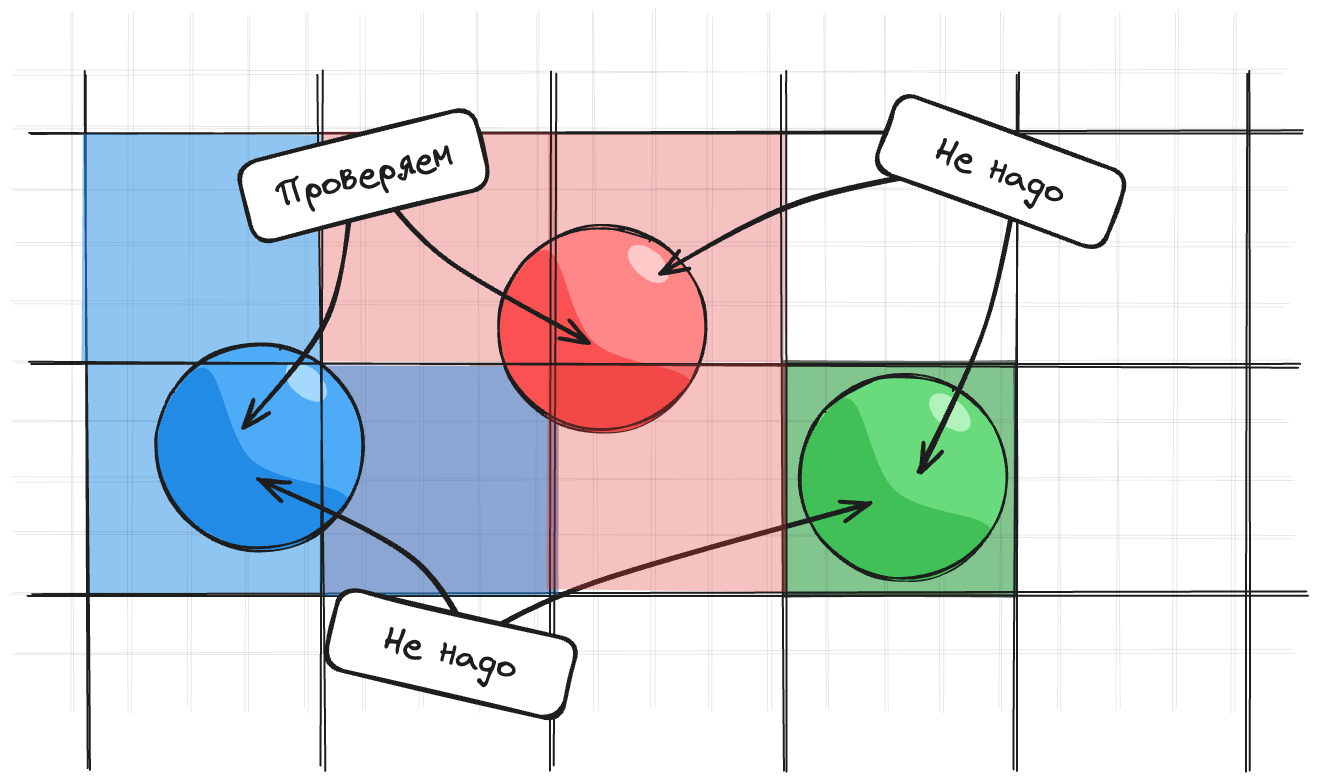

Uniform Grid

Первое, что можно сделать – взять все пространство и разбить его на одинаковые квадраты и хранить все это дело в двумерном массиве.

Получается такая схема:

Симулируем все объекты
Для каждого объекта находим квадрат, в котором он находится и записываем в таблицу
Для каждого квадрата проверяем все объекты в нем и в соседних квадратах
Проверяем коллизии только между объектами которые потенциально могут столкнуться
И так по кругу

И получаем вот такую симуляцию.

Если хранить только центры объектов в одном квадрате (что я и делаю в своем скетче), то ее будет очень просто параллелить. Главное не давать потокам одновременно изменять один и тот же объект.

Grid Map

Когда пространство очень большое, а объектов относительно мало, то массив в котором мы храним объекты не заполнен. Тогда можно использовать хеш-таблицу, чтобы хранить только те квадраты, в которых есть объекты. Квадраты по прежнему одинакового размера, но мы храним только те квадраты, в которых есть объекты.

В остальном схема такая же.

Здесь я храню объекты в квадратах, которые пересекаются с объектом.

Hash Vector

Мапа это динамический структура, которую нужно перестраивать, когда объекты перемещаются. Если объекты быстро перемещаются, то накладные расходы на перестройку могут быть слишком большими. Поэтому используют что-то типо хеш-таблицы с массивом фиксированного размера. Самый популярный подход предложен

Тэкс, давайте по порядку. Раньше у нас был массив, который хранил все пространство. И мы вычисляли индекс квадрата, в котором находится объект, как Index = floor(x / cell_size). Теперь, массив уменьшается в размере и нам нужно придумать функцию, которая будет хешировать координаты объекта в индекс массива.

Index = hash(floor(x / cell_size), floor(y / cell_size))

Для того чтобы Index не выходил за пределы массива, используют функцию берем остаток по модулю от размера массива.

Index = hash(floor(x / cell_size), floor(y / cell_size)) % array_size

Получаем вот такую картину:

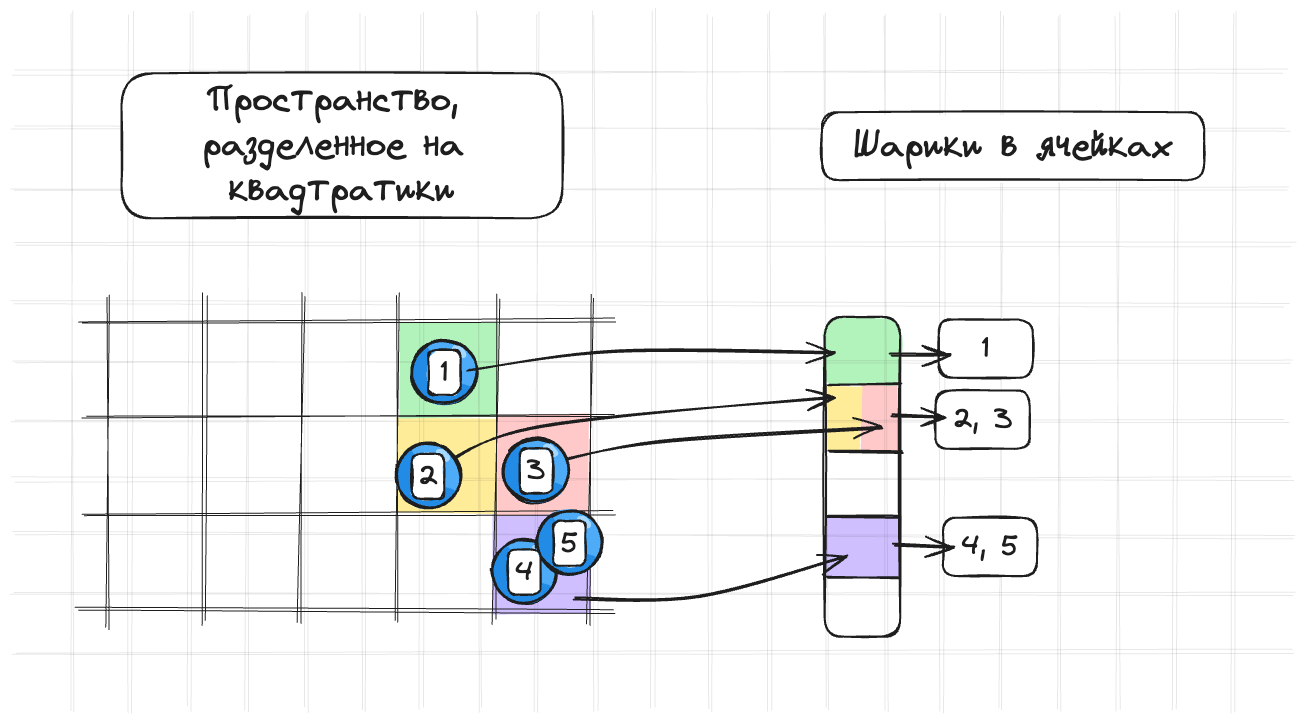
Проходимся по всем объектам
Для каждого объекта вычисляем индекс массива с помощью хеш-функции
В массиве храним набор объектов, которые находятся в квадрате

Иногда у нас может быть коллизия хешей, как это произошло на рисунке: шарики 2 и 3 находятся в разных квадратах, но мы считаем, что в одном. На самом деле чего-то криминального здесь нет. Это грозит нам тем, что мы будем проверять лишние объекты. Тк мы всегда считаем, что объекты находятся в одном квадрате, но на самом деле они в разных.

Вторая проблема от которой мы пытались избавиться – но пока не получилось – динамическая перестройка набора объектов. Каждый раз мы добавляем и удаляем объекты из наборов объектов. Решают эту проблему вот так:

Хранят два массива - первый массив хранит индексы объектов в порядке добавления, второй массив хранит partial sum.

Массив индексов объектов должен быть размера равному количеству объектов. Массив частичных сумм выбираем как удобно. Чем больше массив, тем меньше ситуаций, когда хеш-функция выдает одинаковые значения. Но и тем больше памяти занимает массив. Для того чтобы работал алгоритм частичных сумм, нужно чтобы последняя ячейка массива не относилась ни к одной клетке. Те хэш-функция должна быть такой: hash(x, y) % (array_size - 1)

Для построения такой конструкции делаем следующее:

Проходимся по всем объектам:
- Для каждого объекта вычисляем индекс массива частичных сумм с помощью хеш-функции
- В массиве частичных сумм прибавляем 1 в элементе с этим индексом

   for (let i = 0; i < objects.length; i++) {
        let index = hash(objects[i].x, objects[i].y) % (array_size - 1)
        partial_sum[index] += 1
    }

Получаем вот такую картину:

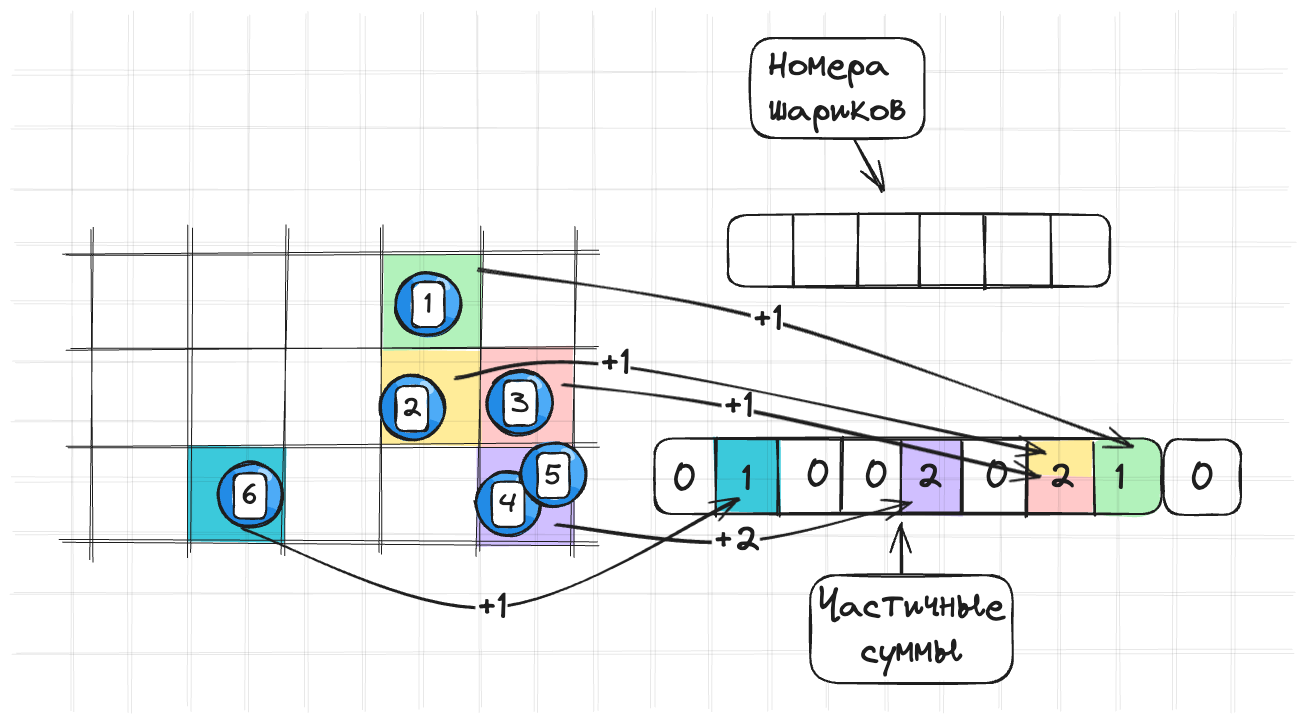
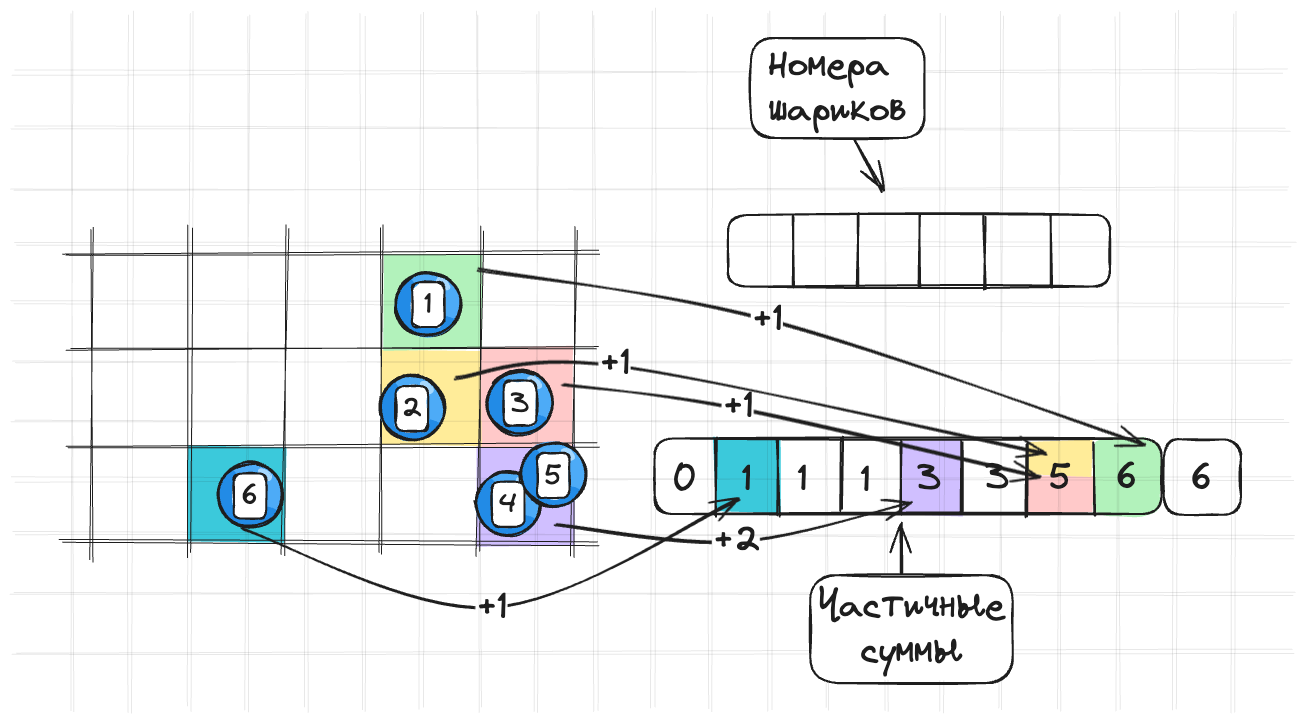
После этого проходимся по массиву частичных сумм и дозаполняем его полностью суммируя все элементы. И получаем вот такую картину:

    for (let i = 1; i < array_size; i++) {
        partial_sum[i] += partial_sum[i - 1]
    }

И потом, заполняем массив индексов объектов:

Проходимся по всем объектам:
- Для каждого объекта вычисляем индекс массива частичных сумм с помощью хеш-функции
- Отнимаем 1 из элемента с этим индексом из массива частичных сумм
- В массиве индексов объектов в элементе с индексом из массива частичных сумм записываем индекс объекта

    for (let i = 0; i < objects.length; i++) {
        let index = hash(objects[i].x, objects[i].y) % (array_size - 1)
        partial_sum[index] -= 1
        index_objects[partial_sum[index]] = i
    }

И получаем финальный результат:

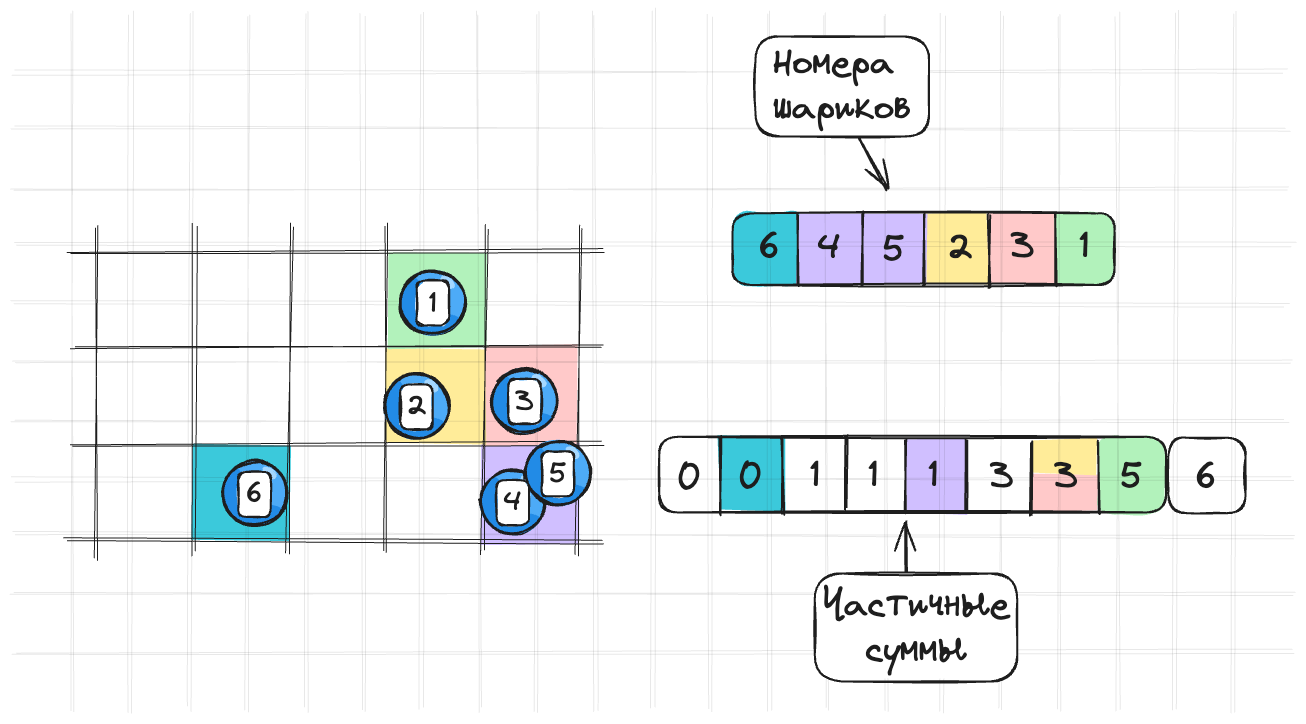
Чтобы узнать какие объекты находятся в ячейке:

Вычисляем индекс массива частичных сумм с помощью хеш-функции
Берем текущую ячейку массива частичных сумм - это индекс в массиве индексов объектов.
Берем разницу между текущей ячейкой и следующей - это количество объектов в ячейке.

    let index = hash(x, y) % (array_size - 1)
    let start =  partial_sum[index]
    let n_objects = partial_sum[index + 1] - start

Чтобы всегда можно было понять сколько элементов в ячейке, мы и добавляли дополнительную ячейку в массив частичных сумм. В принципе можно было обойтись и без него.

Я тут попытался сделать анимацию, но что-то не очень получилось. Как-нибудь попробую снова)

А вот собственно и результат. У меня работает супер быстро.

Заключение

Собственно все. Все это отличные методы, чтобы ускорить проверку. Если у вас они примерно одинакового размера, то будет хорошо работать

Источники

Очень хороший видос от Pezzza’s Work про Uniform Grid
Видос от автора статьи про Hash Vector

1. Bounding Volume