2. Ограничения
Интро
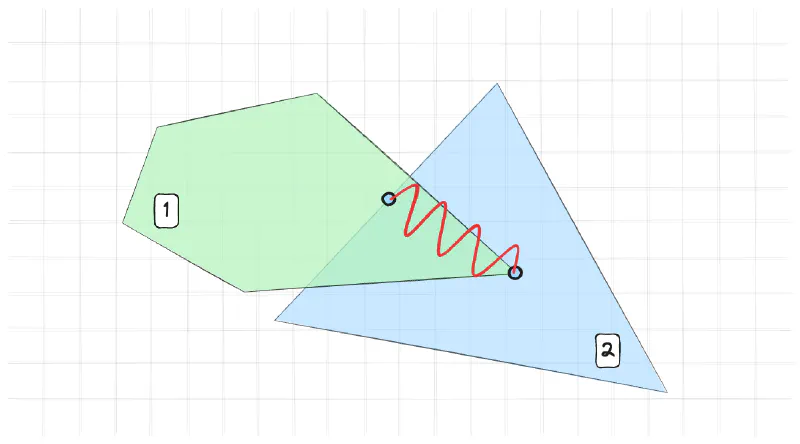
Часто в играх нужно каким-то образом ограничить движение физических объектов. Например, мы хотим сделать рэгдолл, который включается когда персонаж умирает. Его тело должно быть связано в определенных местах, чтобы оно не разлеталось на части. Каждая часть тела не должна проходить сквозь другие части тела и сквозь стены. Колени не должны сгибаться в обратную сторону. Мы хотим чтобы плащ героя был связан с его телом, но при этом мог развеваться на ветру. Или чтобы резиновый шарик не разрушался.
Идейно и не совсем точно, мы можем разделить наши ограничения на жесткие и мягкие.
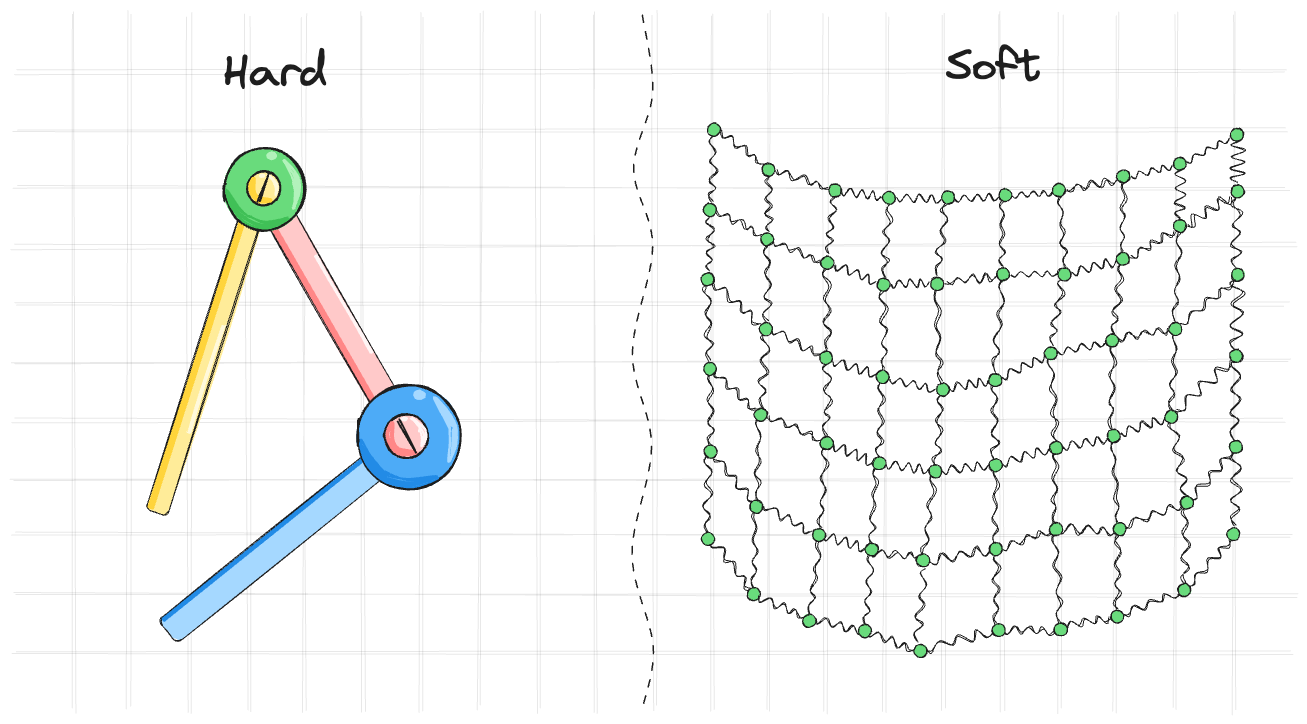
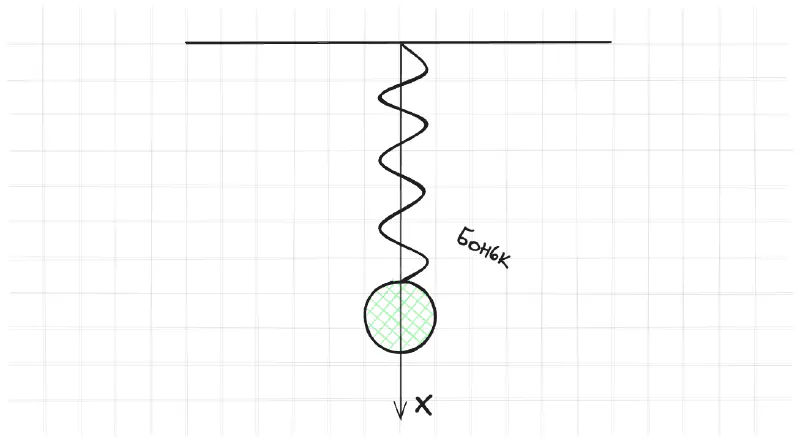
Это разделение нестрогое и зависит от контекста. Но интуиция здесь достаточно простая. Если мы при симуляции допускаем нарушение ограничения, то это мягкое ограничение, если не допускаем, то жесткое. Вот например симуляция резиного шарика. Между точками шарика есть мягкие ограничения на расстояние. Визуально очень хорошо что мы допускаем нарушение длины. В рэгдолле же мы не хотим допускать нарушение длины связей между костями. Будет выглядеть странно, если рука персонажа растянется и будет висеть на нитке.
Формулировка задачи
В основном в физических движках встречаются ограничения которые зависят от координат. Например мы хотим чтобы объекты не проходили друг в друга. Естественно мы можем создавать произвольные ограничения, которые зависят от скоростей, ускорений и т.д. Но они встречаются гораздо реже на практике. Обычно все констрейны пытаются сформулировать в такой форме
$$ \begin{equation} \begin{aligned} C(p_1, p_2,\dots p_n) &= 0 \ \end{aligned} \end{equation} $$
Есть какая-то функция от позиций и она должна быть равна нулю. Если равенство нарушается, значит ограничение нарушено и это нужно исправлять. Например, возьмем просто материальную точку, которая вращается вокруг подвеса.
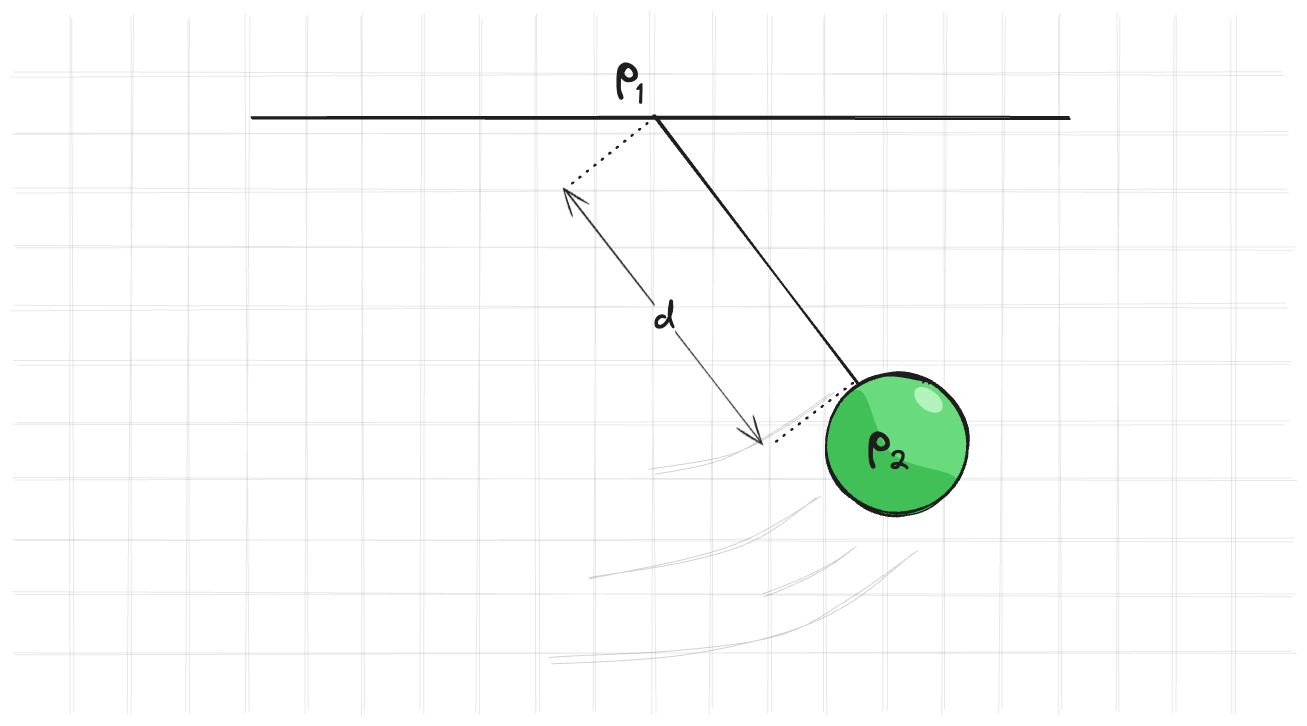
$$ C(p_1, p_2) = |p_1 - p_2| - d = 0 $$
Удовлетворяя этому равенству на каждом шаге мы будем получать вращение точки вокруг подвеса.
Или, например, мы хотим получить что-то похожее на шарик с водой, тогда мы поставим уравнение на сохранение объема
$$ C(p_1, p_2, \dots p_n) = V(p_1, p_2, \dots p_n) - V_0 = 0 $$

Иногда простым равенством не обойдешься. Например, коллизию можно описать только через неравенство.
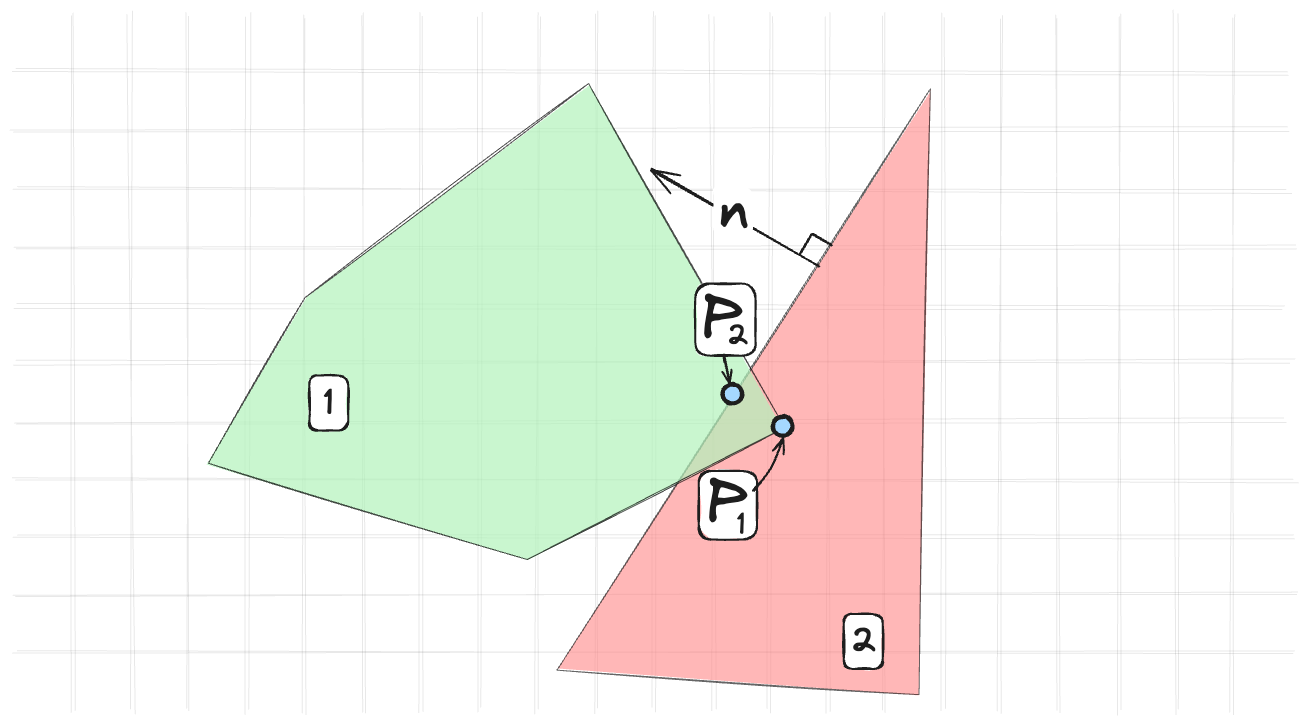
$$ C(p_1, p_2) = (p_1 - p_2)\cdot n \leq 0 $$
Такими уравнениями описывают все ограничения, которые встречаются в симуляции и физический движок должен найти состояние системы, которое удовлетворяет всем ограничениям.
Global vs Local solvers
Все методы решения можно разделить на глобальные и локальные. Глобальные методы решают все ограничения одновременно. Локальные же решают каждое ограничение по отдельности. Я не знаю ни одного игрового движка, который бы использовал глобальные методы. Все используют локальные. Почему? Потому что локальные методы гораздо проще и быстрее. Они не всегда сходятся к решению, но в большинстве случаев это не критично и на это забивают.