2. Метод Hitman Codename 47

Интро

Это супер крутой и очень известный метод, который придумали в 2000 году разработчики игры Hitman: Codename 47. Кажется именно он сильно популяризировал интеграцию Верле. Сейчас он используется в основном в простой симуляции ткани и веревок. Для симуляции твердых и мягких тел его уже не используют. К тому же другой метод который уже используется (XPBD) во многом похож на него. Статья называется Advance Character Physics, но я к ней буду обращаться как к методу Hitman.

Hitman: Codename 47 — одна из первых игр, использовавших (ragdoll) физику, а не готовые анимации для смерти врагов. Вы только посмотрите на эту годноту (Напоминаю это были двухтысячные).

Базово их физический движок выполнял две вещи: интегрировал движение точек и разрешал констрейны между ними.

Чтобы интгрерировать движение они использовали ванильный интегратор Верле. Напомню, что численная схема выглядит так:

$$ \begin{equation} x(t + \Delta t) = 2x(t) + x(t - \Delta t) + a(t)\Delta t^2 \end{equation} $$

Как уже говорилось, в нем нет скоростей в явном виде.

Для того чтобы разрешать констрейны они придумали процедуру релаксации. В этой релаксации и есть вся изюминка метода.

Псевдокод симуляции

function simulate(points, constraints, iterations = 10) {
  // Интегрируем по Верле
  for (let point of points) {
    point.integrate();
  }
  // Разрешаем констрейны несколько раз
  for (let i = 0; i < iterations; i++) {
    for (let constraint of constraints) {
      constraint.relax();
    }
  }
}

Релаксация

Идея релаксации очень простая. Когда какие-то позиции не удовлетворяют ограничениям, мы их просто сдвигаем так, чтобы ограничения выполнялись. Вопрос в том. как это правильно делать.

Пример

Сначала разберемся с релаксацией на простых примерах. Вот есть две точки, которые должны быть на расстоянии $d$ друг от друга.

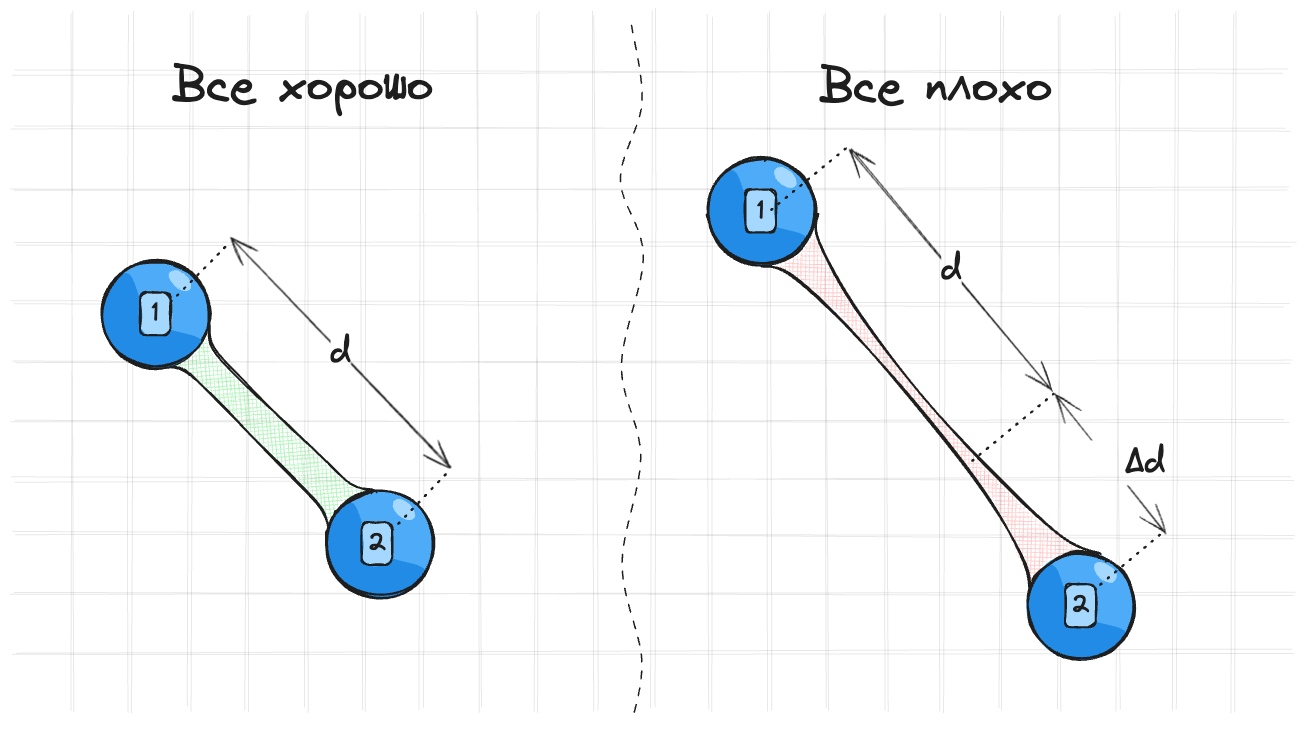
Ограничение на сохранение растояния между двумя точками:

$$ \begin{equation} C(\vec{p_1}, \vec{p_2}) = |\vec{p_2} - \vec{p_1}| - d = 0 \end{equation} $$

В какой-то момент симуляции мы получаем плохую ситуация с растянутым ограничением. Точки оказались дальше, чем нужно. В таком случае релаксация должна стянуть точки к друг другу чтобы выполнить ограничение. Мы можем удовлетворить это ограничение множеством способов, поэтому нужно ввести дополнительные условия: Смещение должно быть минимальным в направлении к центру масс. Поэтому логично смещать точки друг к другу. В оригинальной статье еще не было математического обоснования для такого выбора, авторы действовали интуитивно. Позднее в статье о XPBD будет более строгое обоснование.
Для точек с одинаковой массой можно каждую сместить на половину сдвига:

$$ \begin{equation} \begin{split} &\vec{p^{new}_1} = \vec{p_1} - \frac{1}{2}\Delta d \\ &\vec{p^{new}_2} = \vec{p_2} + \frac{1}{2}\Delta d \end{split} \end{equation} $$

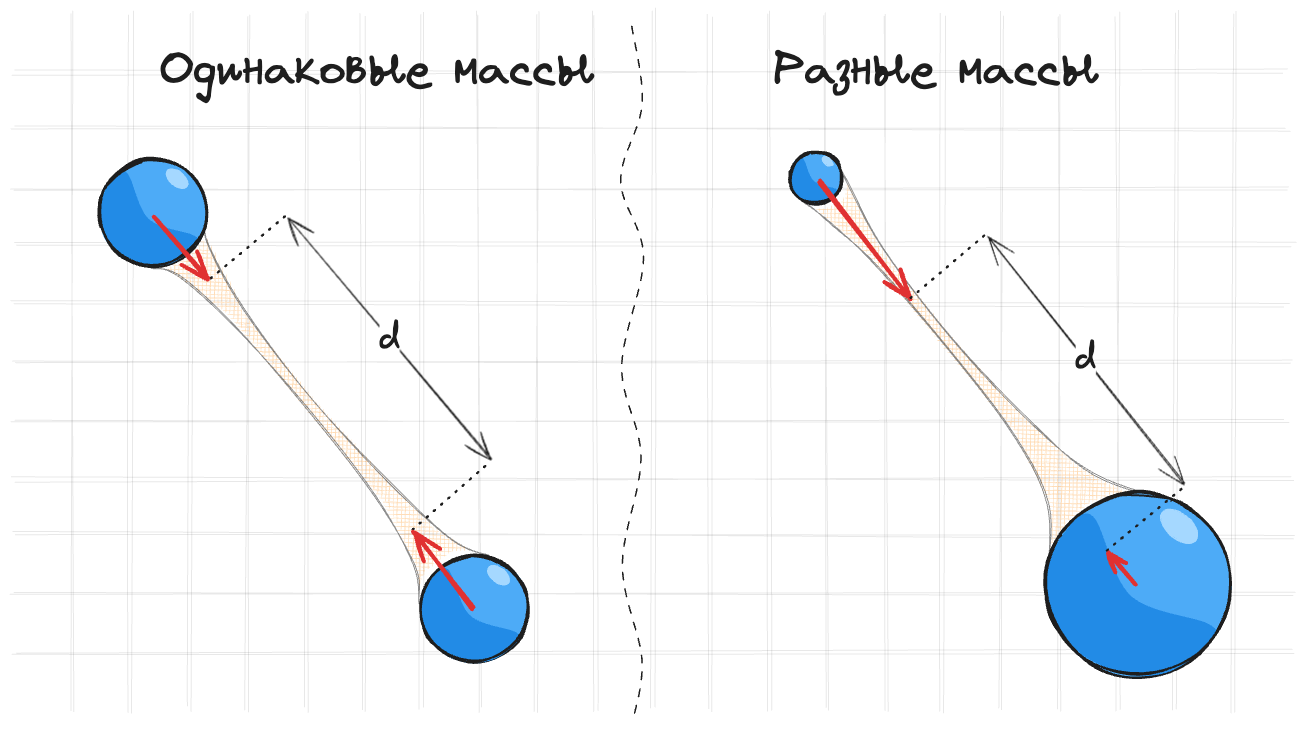
Для точек с разной массой можно каждую сместить на величину, обратно пропорциональную массе:

$$ \begin{equation} \begin{split} &\vec{p^{new}_1} = \vec{p_1} - \frac{m_2}{m_1 + m_2}\Delta x \\ &\vec{p^{new}_2} = \vec{p_2} + \frac{m_1}{m_1 + m_2}\Delta x \end{split} \end{equation} $$

для того чтобы тело с большей массой было более инертным и смещалось меньше.

Обобщаем

Теперь попробуем обобщить этот метод на случай, когда у нас несколько точек и несколько ограничений. Вот 4 материальные точки и 6 ограничений, некоторые растянуты, некоторые сжаты.

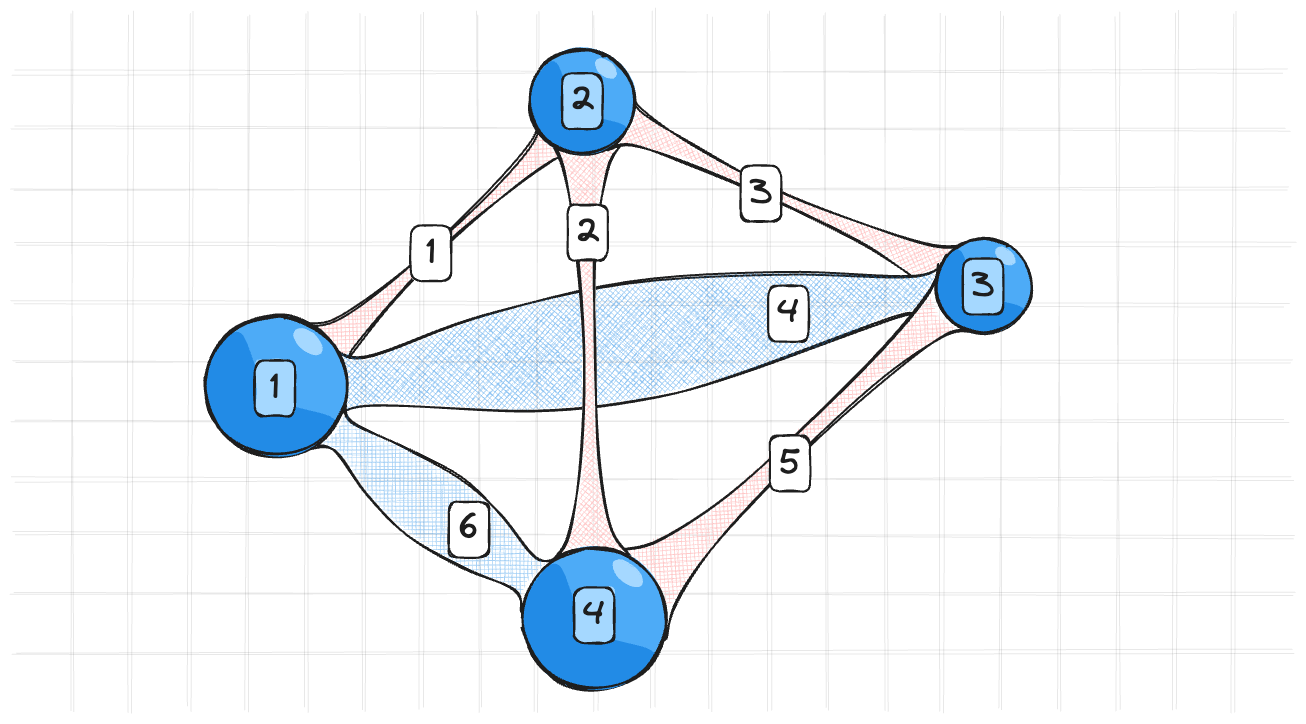
Мы не умеем решать такую систему с несколькими точками, но нам это и не нужно. Оказывается если разрешать ограничения по одному несколько раз, то получается хороший результат. Если мы возьмем много материальных точек создадим из них шар и создадим между ними ограничения, а потом сожмем, то вот что получится:

Вот так будет выглядеть релаксация системы. Ее явный плюс в том, мы можем остановиться на любой итерации и таким образом регулировать точность выполнения ограничения и затраты на вычисления.

Ограничение углов

Чтобы симулировать рэгдолл нужно уметь ставить ограничения на углы.

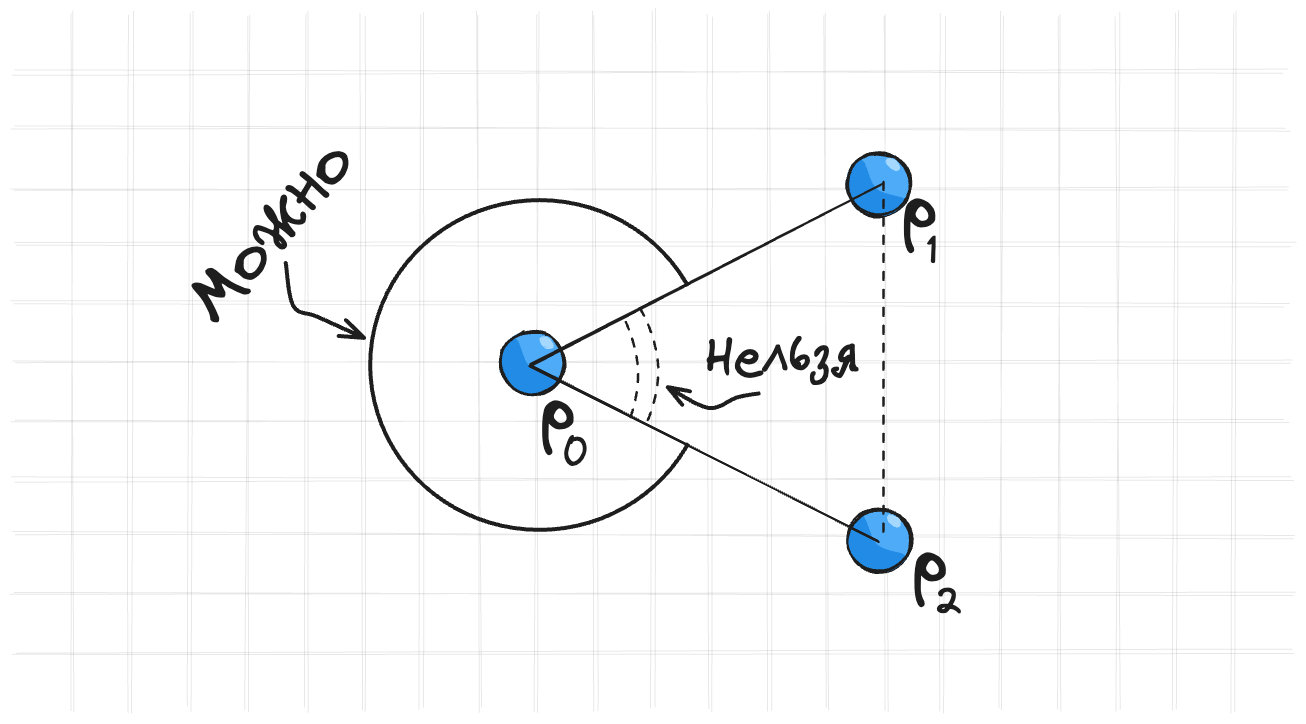
Для таких ограничений предлагают несколько вариантов:

Включать обычное ограничение на расстояние между точками $\vec{p_1}$ и $\vec{p_2}$ только когда расстояние между ними меньше $d$.

$$ \begin{equation} C(\vec{p_1}, \vec{p_2}) = |\vec{p_2} - \vec{p_1}| - d > 0 \end{equation} $$

Такое ограничение не совсем удобно настравить тк нужно пересчитывать расстояние между точками при настройке системы.

Включать ограничение на угол между точками $\vec{p_1}$, $\vec{p_2}$ и $\vec{p_3}$ только когда угол между ними больше $\theta$.

$$ \begin{equation} С(\vec{p_0}, \vec{p_1}, \vec{p_2}) = (\vec{p_1} - \vec{p_0}) \cdot (\vec{p_2} - \vec{p_0}) - cos(\theta) < 0 \end{equation} $$

Насколько я понимаю авторы воспользовались первым вариантом, тк он проще и уже известно, как его разрешать. Со вторым вариантом не совсем понятно, что делать. Но в следующей статье мы разберемся, как разрешать ограничение произвольного типа.

Приближение корня

В текущей релаксации мы очень много раз считаем растояние между двумя точками и для этого нам приходится считать корень. Чтобы сэкономить на этом в статье вычисляют не честный корень, а его аппроксимацию. Если обозначить $d = \vec{p_2} - \vec{p_1}$

$$ \begin{equation} \sqrt{\vec{p^2_2} - \vec{p^2_1}} \approx d*(\frac{r^2}{d^2 + r^2} - 0.5) \end{equation} $$

Где $r$ - расстояние между точками заданное в ограничении (restlength), $\delta$ - текущее расстояние между точками.

Разрешение коллизий

Отлично, мы научились разрешать ограничения на позиции. Теперь попробуем разрешить коллизию. Если точка прошла сквозь стенку, то мы можем просто сдвинуть ее обратно на место. Получается тоже отлично.

На 12 проходе можно и останавливаться.

И по итогу получаем очень устойчивую симуляция с неупругим столкновением (Если полностью разрешать систему).

В такой схеме если не до конца разрешать ограничения, порядок разрешения ограничений будет влиять на результат. Попробуйте поставить мало итераций и много точек и посмотреть что будет. Тело должно начать вращаться то в одну сторону, то в другую.

Вот на простом квадрате можно увидеть как это будет приводить к повороту.

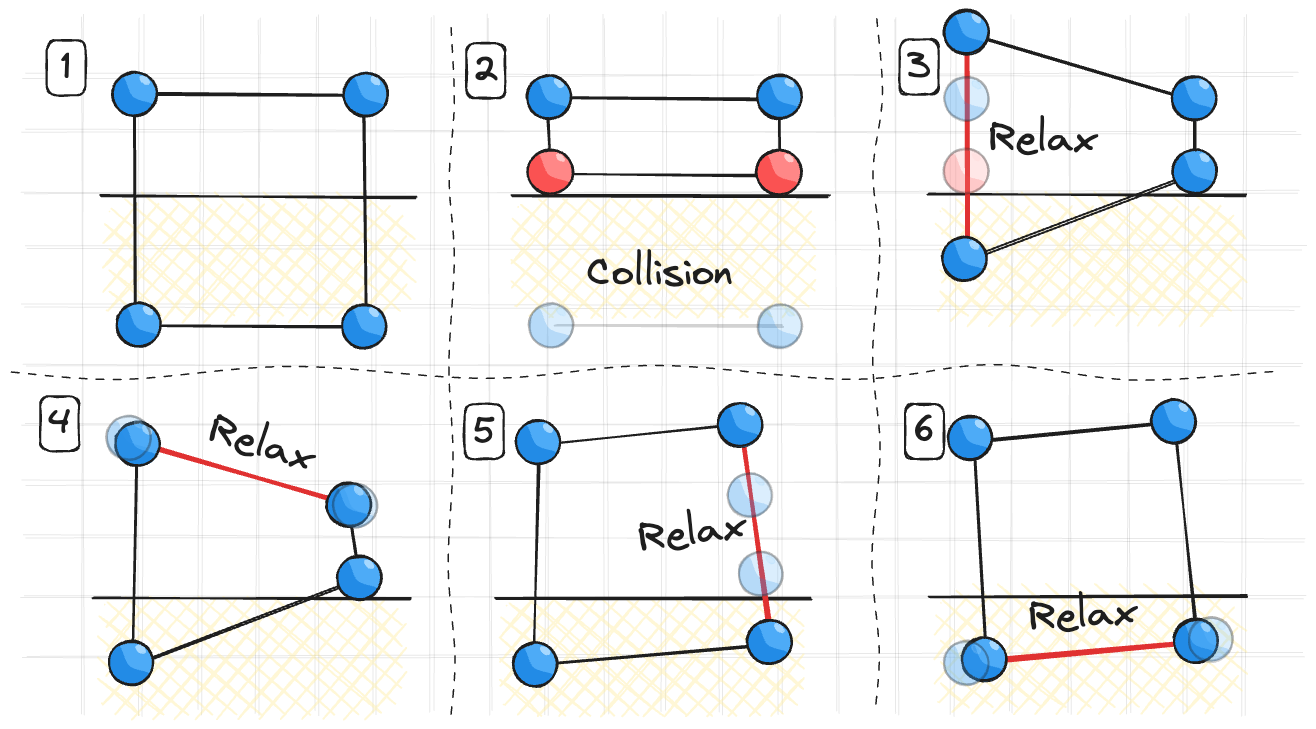
Сначала разрешаются коллизии, потом по очереди по часовой стрелке ограничения на длину сторон. После первой итерации квадрат повернут.

Я не видел в статье решения этой проблемы но сообщество говорит о том, что нужно просто разрешать ограничения в случайном порядке.

Коллизия с углом

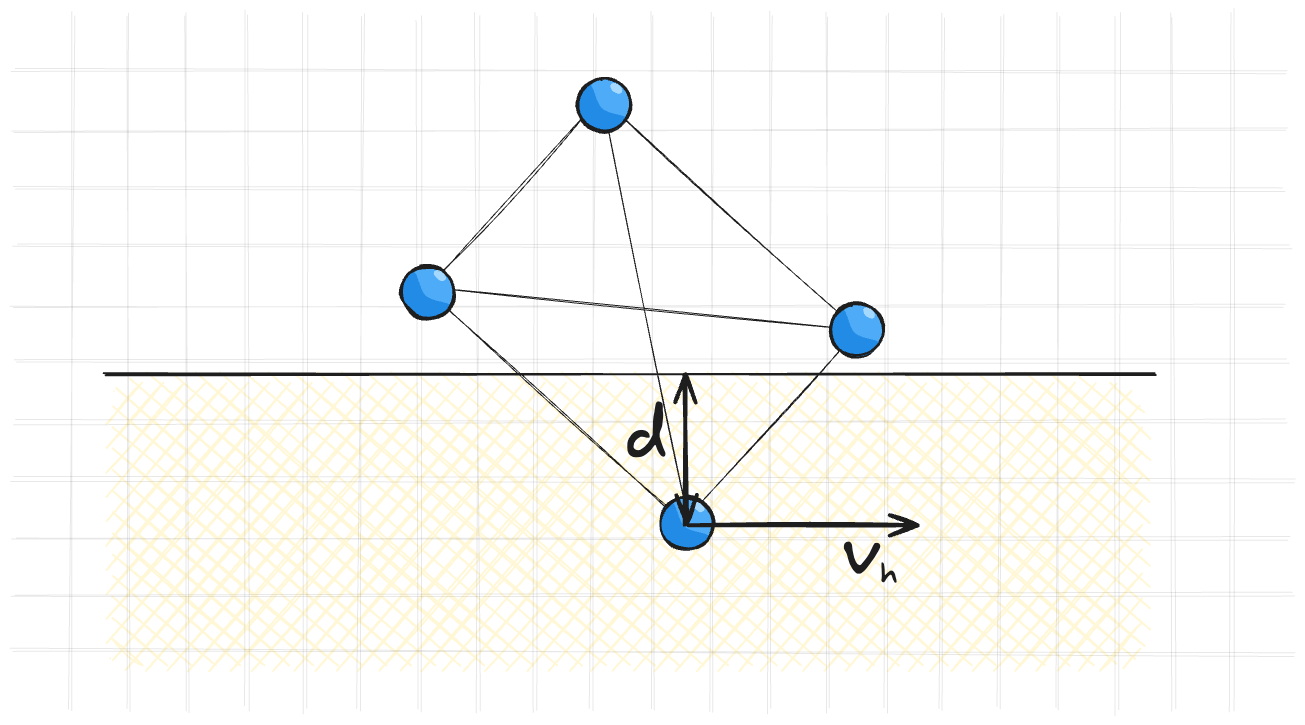
Тело составленное из ребер и поинтов может ударяться не только поинтом, но и ребром. До сих пор мы рассматривали только коллизии с поинтами. Если поинт колизится с чем-нибудь, то мы просто его выталкиваем. Но что делать если ребро коллизирует с чем-то?

Для того чтобы такая коллизия хорошо смотрелась нельзя просто вытолкнуть ребро вверх по нормали

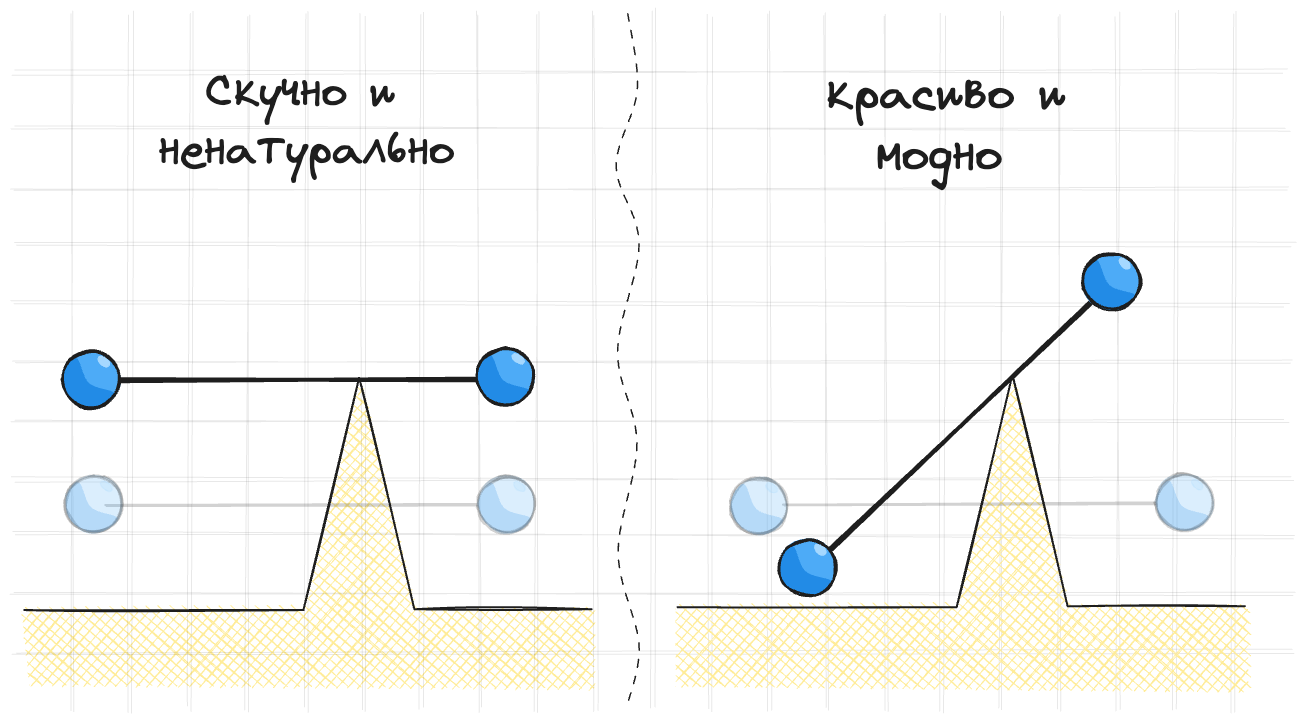
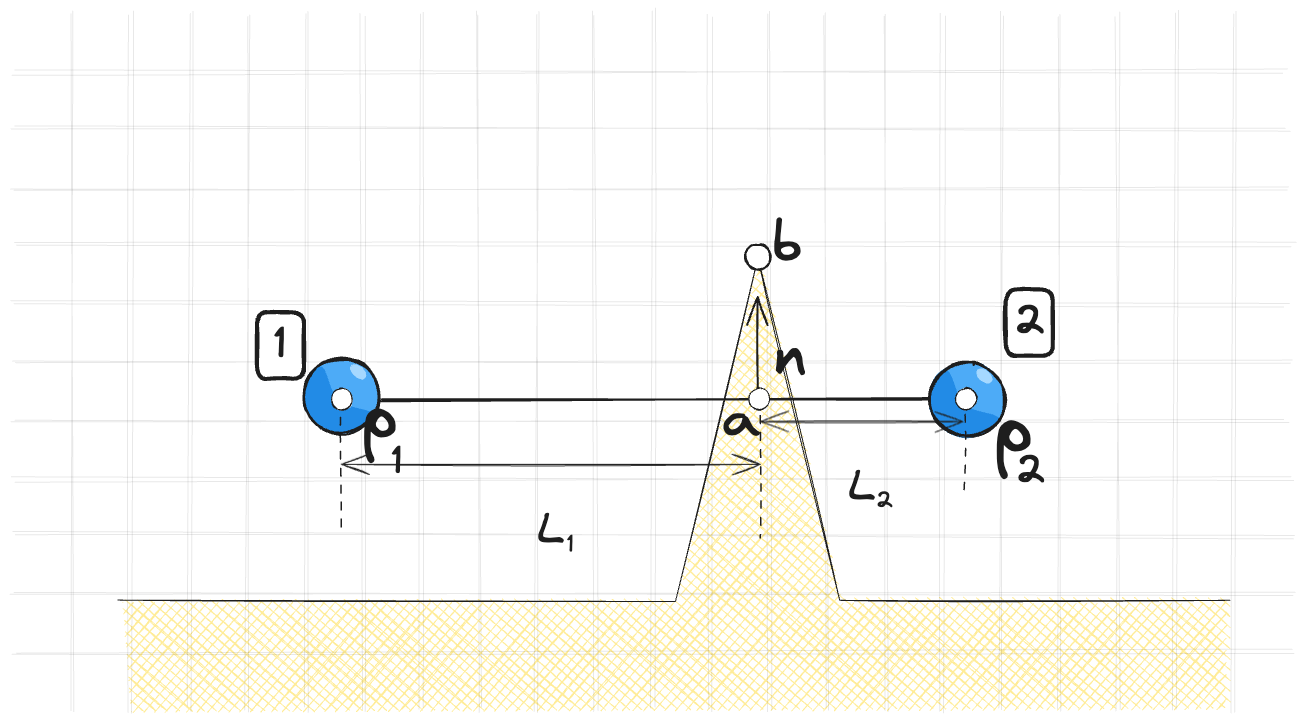
Для этого точки сдвигают учитывая длины рычагов $L_1$ и $L_2$. Чтобы не иметь делов с поворотом точки сдвигают по нормали. Из-за этого длина может нарушиться, но это уже решится при разрешении ограничений на длину.

Итак мы можем представить точку $a$ как линейную комбинацию точек $\vec{p_1}$ и $\vec{p_2}$:

$$ \begin{equation} a = c_1 * \vec{p_1} + c_2 * \vec{p_2} \end{equation} $$

Где $c_1$ и $c_2$ - коэффициенты линейной комбинации

$$ \begin{equation} c_1 = \frac{L_2}{L_1 + L_2} \quad c_2 = \frac{L_1}{L_1 + L_2} \end{equation} $$

Мы хотим найти новые позиции точек $\vec{p^{new}_1}$ и $\vec{p^{new}_2}$ так чтобы точка $\vec{a^{new}}$ совпадала с точкой $\vec{b}$:

$$ \begin{equation} \vec{a^{new}} = b = c_1 * \vec{p^{new}_1} + c_2 * \vec{p^{new}_2} \end{equation} $$

Если ввести вектор нормали $n = b - a$ то можно переписать уравнения в виде

$$ \begin{equation} \begin{split} &\vec{p^{new}_1} = \vec{p_1} + c_1 * \lambda n \\ &\vec{p^{new}_2} = \vec{p_2} + c_2 * \lambda n \end{split} \end{equation} $$

Вывод лямбды

$$ \begin{equation} \begin{split} &a^{new} = b \Rightarrow a^{new} * n = b * n = \dots \\ &= (c_1 * p^{new}_1 + c_2 * p^{new}_2) * n = \dots \\ &= (c_1 * (\vec{p_1} + c_1*\lambda * n) + \\ &c_2 * (\vec{p_2} + c_2*\lambda * n)) * n = \dots \\ &= b * n + \lambda * (c_1^2 + c_2^2) * n^2 \end{split} \end{equation} $$

И вот так мы можем найти $\lambda$:

$$ \begin{equation} \lambda = \frac{1}{c_1^2 + c_2^2} \end{equation} $$

И подставляя $\lambda$ в уравнения для $\vec{p^{new}_1}$ и $\vec{p^{new}_2}$ получим новые позиции точек.

Упругое столкновение

Если делать разрешение коллизий по статье, то можно получить неупругое столкновение. (Ну или слегка упругое, если итераций недостаточно). И здесь не совсем понятно, как не имея скорости в явном виде сделать упругое столкновение. В статье этого нет, но вот простой способ:

Что происходит сейчас:

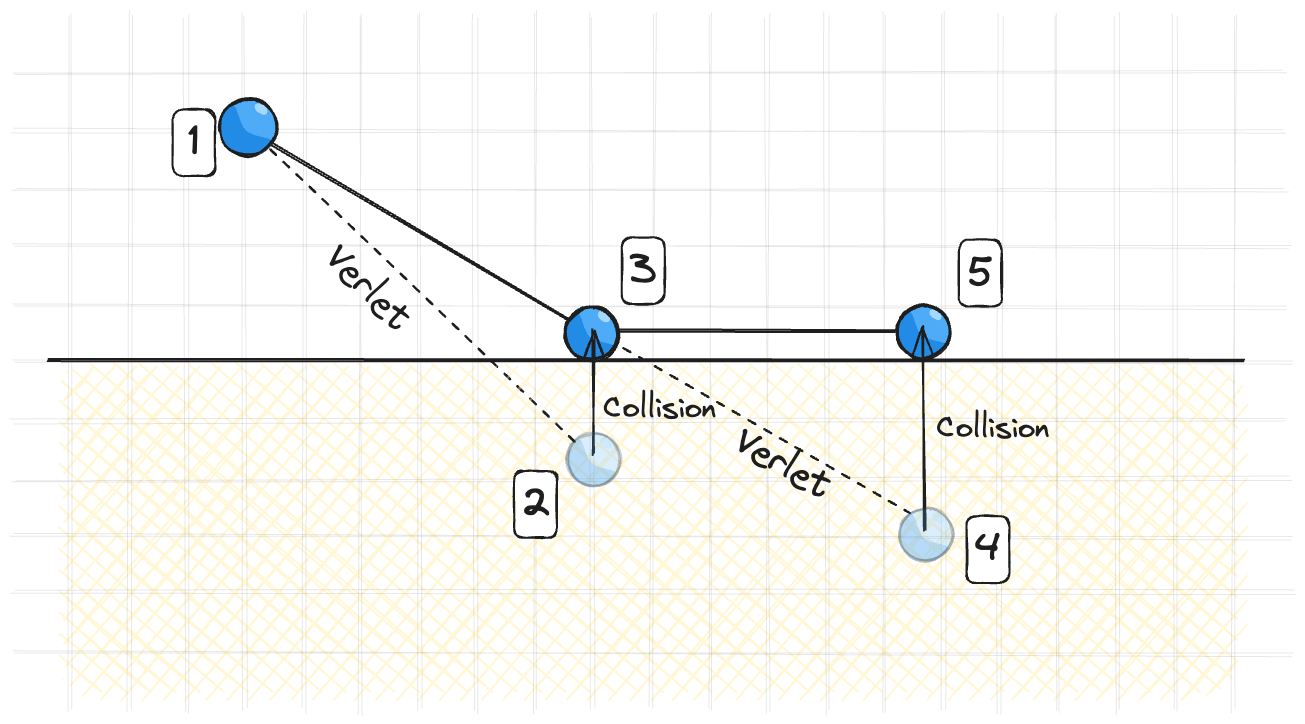
Шарик летит и в какой-то момент натыкается на стенку. Он проникает в нее (2). После этого разрешение коллизиии выталкивает его (3) И симуляция продолжается. Шарик летит из положения (3) с учетом предыдущей позиции (1) и тд. Получается неупругое столкновение.

Чтобы сделать упругое столкновение можно поступить вот так:

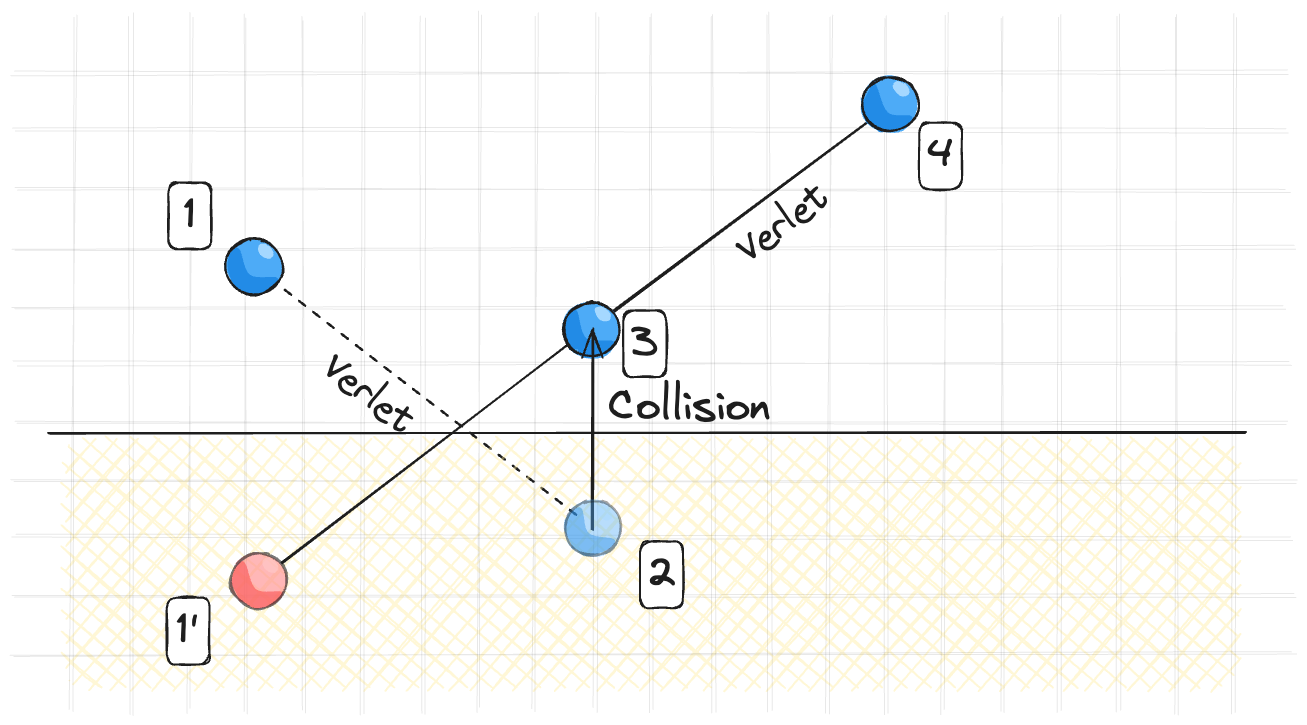
После того как шарик врезался в пол при разрешении коллизий его нужно вытолкнуть на расстояние равное глубине проникновения и переписать предыдущее положение шарика на (1’) (Зеркально отраженное). Тогда не следующей итерации шарик будет лететь в другую сторону. На мягких телах алгоритм работает приемлемо, но он плохо сработает при симуляции твердого тела. Это всего лишь способ управлять скоростью в ванильном Верле. Собственно, из-за таких неудобств и переходят на схемы, где скорость есть в явном виде.

Трение

В статье говорится, о том что нужно уменьшать скорость частицы пропроционально глубине ее проникновения в поверхность. Мне не совсем понятно, что имелось ввиду, ведь в ванильном Верле нет скорости в явном виде.

Но мы можем храним предыдущую позицию и для того чтобы уменьшить скорость частицы, мы можем предыдущую позиции пододвинуть к текущей. И вот так можно уменьшить скорость частицы.

Симуляция ткани

Этим методом можно симулировать ткань если вызывать немного итераций. А для того чтобы можно было регулировать эластичность ткани, можно на каждой итерации восстанавливать ограничение не полностью, а на какой-то процент. А еще можно убирать констрейн, если он слишком сильно растягивается и таким образом рвать ткань. В общем зацените:

Таким же образом можно симулировать мягкие тела.

Successive over-relaxation

Я не придумал, как это перевести, поэтому буду по angliski. В статье об этом тоже не говорится, но это простой способ ускорить сходимость релаксации. Идея в том, что мы можем сдвигать точки не на половину сдвига, а на большую величину. Это очень сильно может ускорить сходимость.

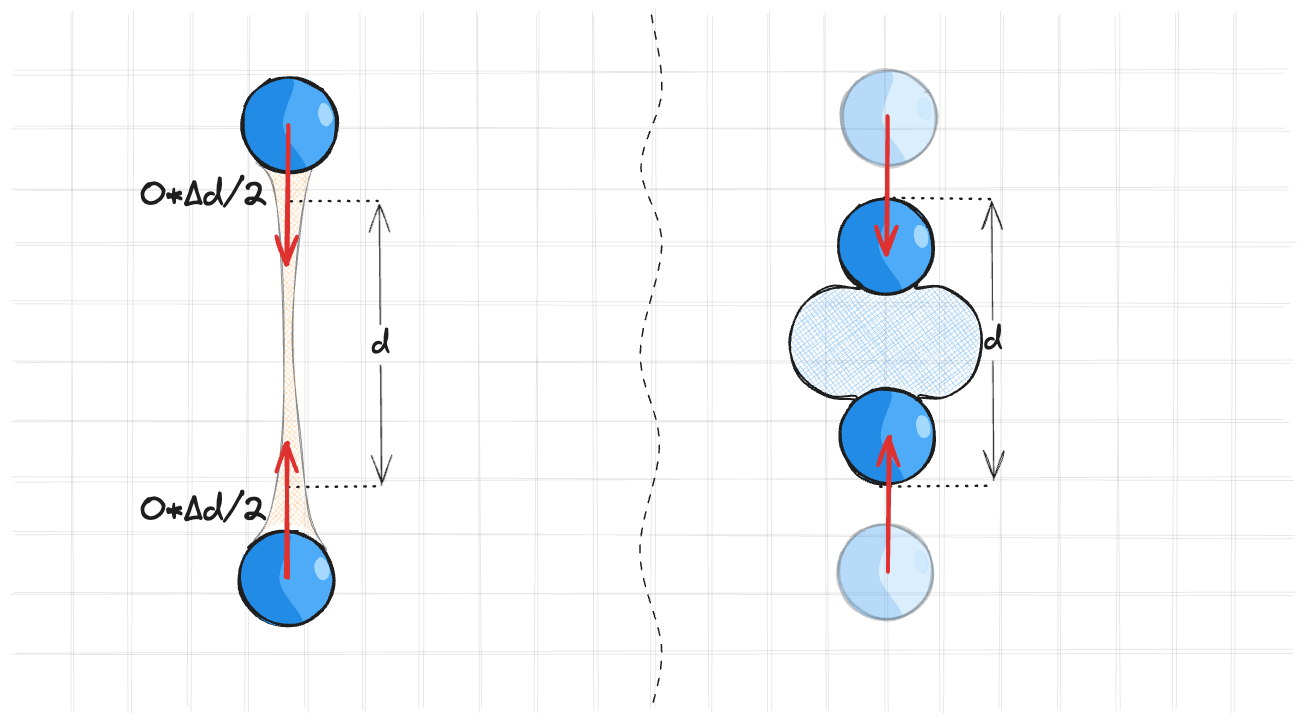
Но нужно не забывать, что она может делать менее стабильной релаксацию, поэтому лучше всего использовать метод на первых итерациях релаксации.

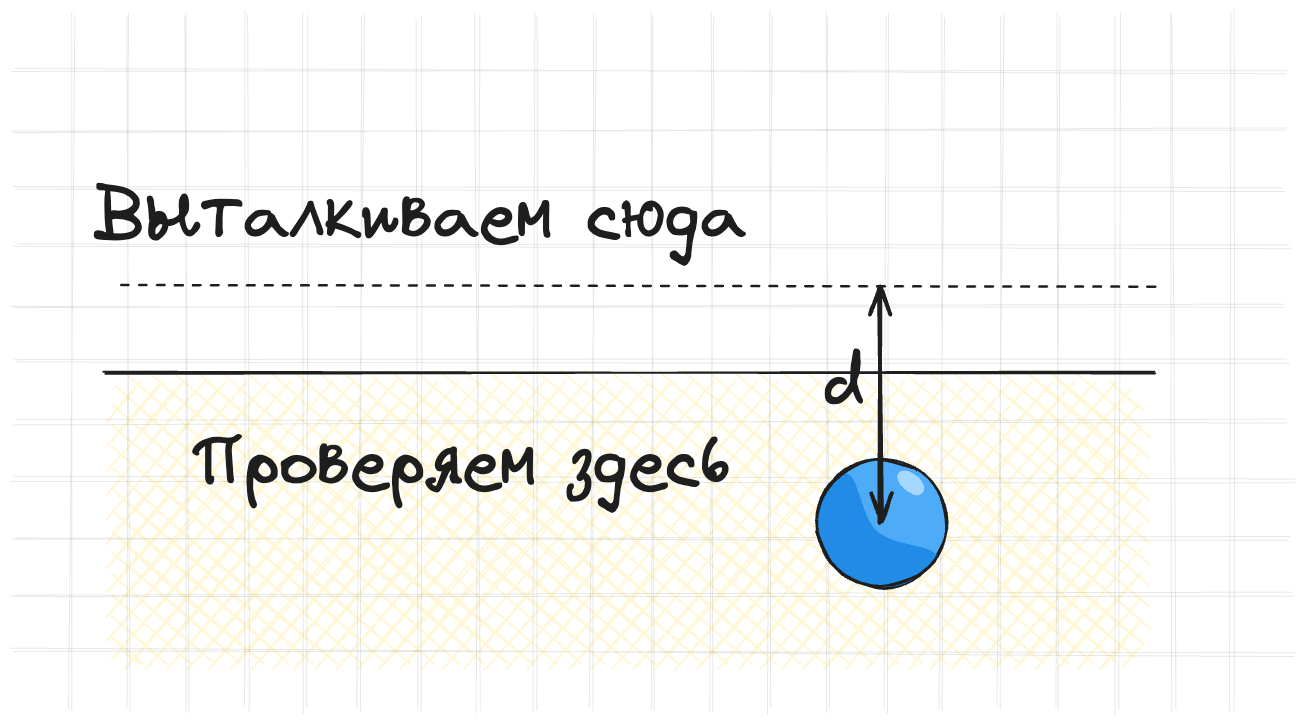
Если для хорошего результата раньше нам нужно было 12 релаксаций, то с overrelaxation нам хватит 6.

А для коллизий можно вообще добавить постоянный дополнительный отступ. Те выталкивать дальше чем нужно. Это ускорит сходимость.

Заключение

Крутой и простой метод, который приятно прогать. В отличии от penalty method его гораздо труднее поломать (просто следите чтобы не было деления на ноль). Если нужна простая симуляция тканей или веревок, то этот метод подойдет. Вот даже по слухам в Horizon Forbidden West использовали его. Простые симуляцие твердых тел, тоже прокатят, но если нужно что-то более сложное, то лучше использовать другие методы. Тк в данном нужно будет много итераций чтобы получить хороший результат.

Источники

1. Penalty method 3. PBD