3. PBD

Интро

Это первая статья в серии XPBD. Она является логичным продолжением метода hitman. Была написана в далеком 2006. Зацените видос Position Based Dynamics.

Псевдокод симуляции

function simulate() {
  // Расчет ускорений; Обычно это только гравитация
  for (let point of points) {
    point.a = calculateAcceleration(point);
  }
  for (let point of points) {
    // Интегрируем скорости
    point.v += point.a * dt;
    // Дэмпинг скорости
    dampVelocity(point.v);
    // Интегрируем позиции и записываем их в p
    point.p = point.x + point.v * dt;
  }
  // Расчитываем коллизии один раз
  addCollisionConstraints(points);
  // Разрешаем все констрейны и коллизии и изменяем позиции точек p
  for (let i = 0; i < iterations; i++) {
    for (let c of constraints) {
      resolveConstraint(c);
    }
  }
  // обновляем позиции и скорости точек после разрешения ограничений
  for (let point of points) {
    point.v = (point.p - point.x) / dt;
    point.x = point.p;
  }
  // обновляем скорости точек после разрешения коллизий
  // и добавляем трение и упругость
  for (let point of points) {
    updateVelocity(point.v);
  }
}

Обращаю внимание что мы храним две позиции. $x$ и $p$. $x$ это текущая позиция точки. $p$ это позиция точки на следующем шаге.

Интегратор

Первое улучшение – это использование другого интегратора. В прошлом методе было сложно добиться хороших и сочных упругих коллизий. В основном мы получали неупругое столкновение, из-за того что не могли управлять скоростью В PBD Вместо Vanilla Euler используется Symplectic Euler. Напомню, что Symplectic Euler выглядит так:

$$ \begin{equation} \begin{split} v_{i+1} = v_i + \Delta t \cdot a_i x_{i+1} = x_i + \Delta t \cdot v_{i+1} \end{split} \end{equation} $$

В этом интеграторе есть скорость в явном виде. И это позволяет без всяких костылей управлять скоростью. Поэтому можно просто сделать вот такое упругое столкновение.

Универсальное решение

В статье Hitman авторы придумывали разные методы для разрешения ограничений. И математического обоснование под это не было. Они действовали скорее интуитивно. В PBD предлагают универсальное решение по тому как лучше всего разрешать ограничения $C(\vec{p})$.

Для того чтобы разрешить уравнение нужно найти такое $\Delta \vec{p}$, чтобы $C(\vec{p} + \Delta \vec{p}) = 0$. Здесь $\vec{p}$ – конкатенация всех позиций всех точек. Те если у нас есть два шарика, то $\vec{p} = [x_1, y_1, x_2, y_2]$.

Для произвольного ограничения мы не можем так просто его найти, поэтому делают стандартное разложение в ряд Тейлора и оставляют только первые два члена.

$$ \begin{equation} C(\vec{p} + \Delta \vec{p}) \approx C(\vec{p}) + \nabla_{\vec{p}} C(\vec{p}) \cdot \Delta \vec{p} = 0 \end{equation} $$

Если бы это было обычное уравнение, то мы бы его запросто решили. Но тут векторы и получается проблемка. Предположим, что $C(\vec{p}) = c$ и $\nabla_{\vec{p}} C(\vec{p}) = [a, b]$ и $\Delta \vec{p} = [x, y]$. Тогда у нас получится такое уравнение:

$$ a * x + b * y = -c $$

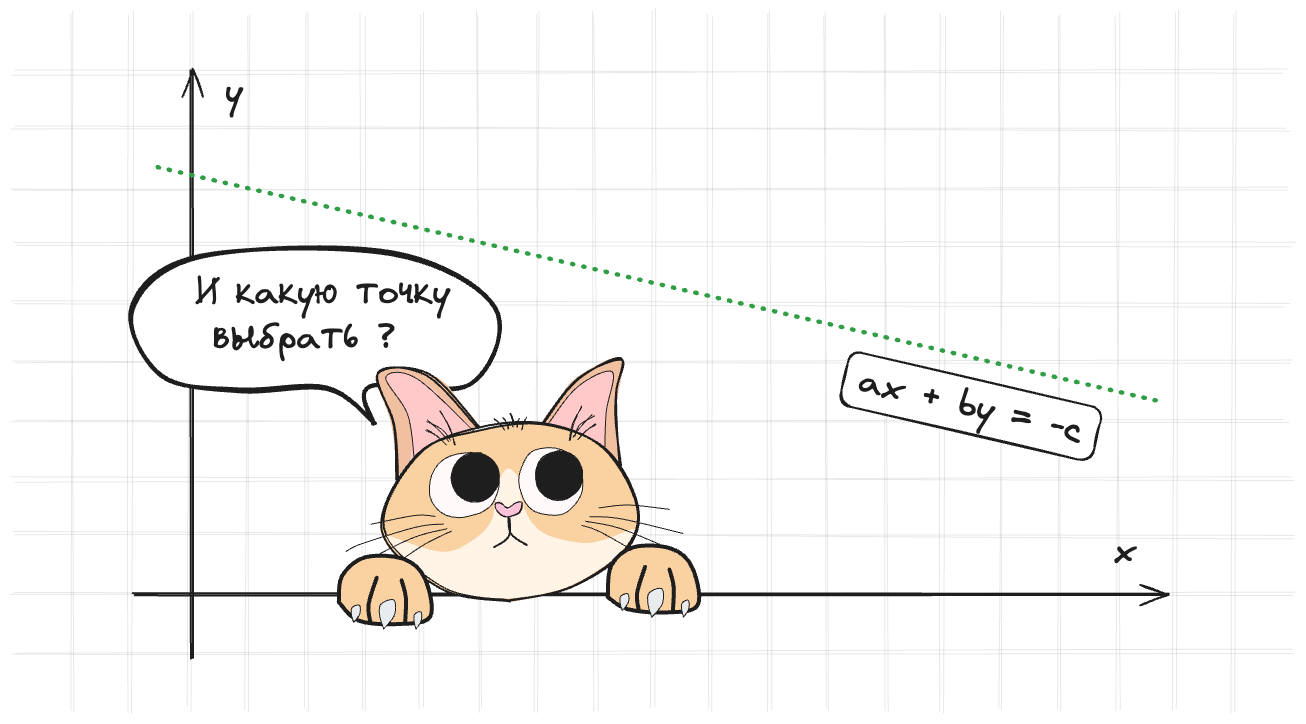
Собственно это уравнение прямой. Для того чтобы найти однозначное решение, нужно добавить еще одно ограничение.
В качестве него мы можем требовать чтобы $\Delta \vec{p}$ была сонаправлена с градиентом. Т.е $\Delta \vec{p} = \lambda \nabla_p C(\vec{p})$.

Почему так, можно понять на простом примере. Вот у нас есть маятник. Он должен сохранять расстояние до подвеса. И мы пытаемся найти новую позицию для шарика. Самое логичное решение – это двигать шарик по самому короткому пути к второму шарику. Т.е по направлению градиента.

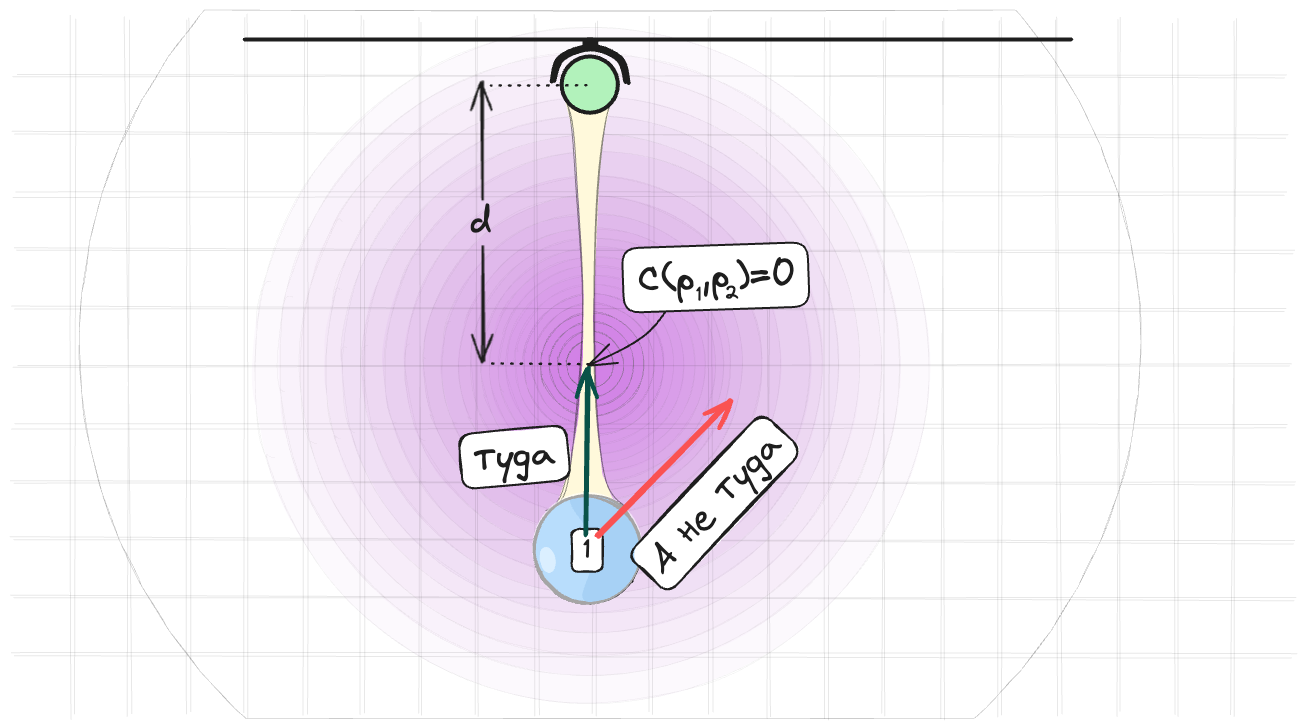
С дополнительным уравнением можно получить решение

$$ \begin{equation} \Delta \vec{p} = -\frac{C(\vec{p})}{\nabla_p C(\vec{\vec{p}}) \cdot \nabla_p C(\vec{p})} \nabla_p C(\vec{p}) \end{equation} $$

Для того чтобы было удобнее считать, нужно разбить $\vec{p}$ на $\vec{p_1}, \dots, \vec{p_n}$, можно переписать решение для конкретной $\vec{p_i}$ и разрешить ограничение вида $C(\vec{p_1}, \dots, \vec{p_n})$ нужно переписать уравнение вот так:

$$ \begin{equation} \begin{split} &\Delta \vec{p_i} = -s * \nabla_{\vec{p_i}} C \\ &s = \frac{C}{\sum_{k} (\nabla_{\vec{p_k}} C)^2} \end{split} \end{equation} $$

Пытаемся понять

Расчет $\Delta \vec{p}$ состоит из двух частей. Первая часть – это градиент ограничения: $-\nabla_{\vec{p_i}} C(\vec{p})$ – Это вектор, который показывает в какую сторону нужно двигаться чтобы уменьшить ограничение. Собственно, это то что я показывал на прошлом рисунке.

Вторая часть – это коэффициент $s$. Он показывает насколько сильно нужно двигаться в этом направлении. Знаменатель в нем означает, что чем больше точек участвует в ограничении, тем меньше нужно двигаться каждой точке.

Давайте на примере. Вот у нас есть ограничение на площадь десятиугольника. $C(\vec{p_1}, \dots, \vec{p_{10}}) = S - S_0$.

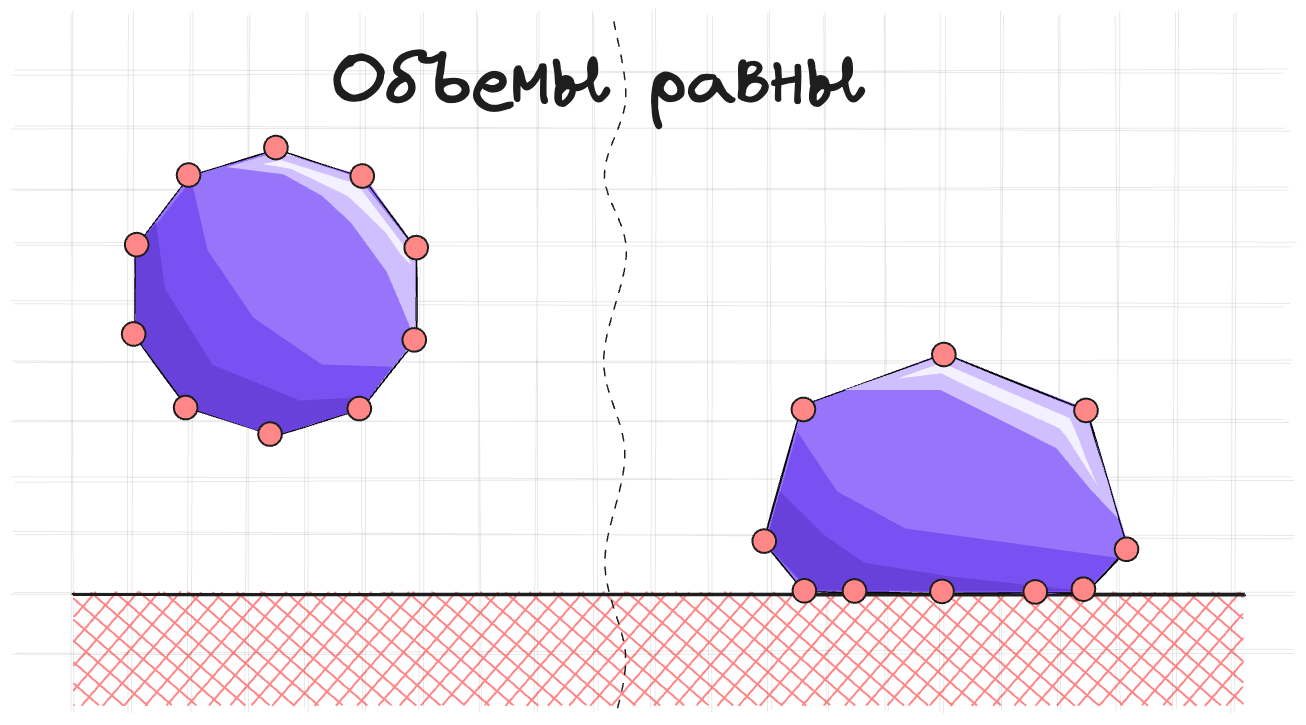
И давайте предположим, что эту фигуру равномерно сжало. Нужно восстановить площадь. Этого можно добиться несколькими способами: Например, подвинуть одну точку очень сильно, а остальные вообще не двигать. Или можно подвинуть все точки немного. Если у точек одинаковая масса, то второй вариант просто логичнее.

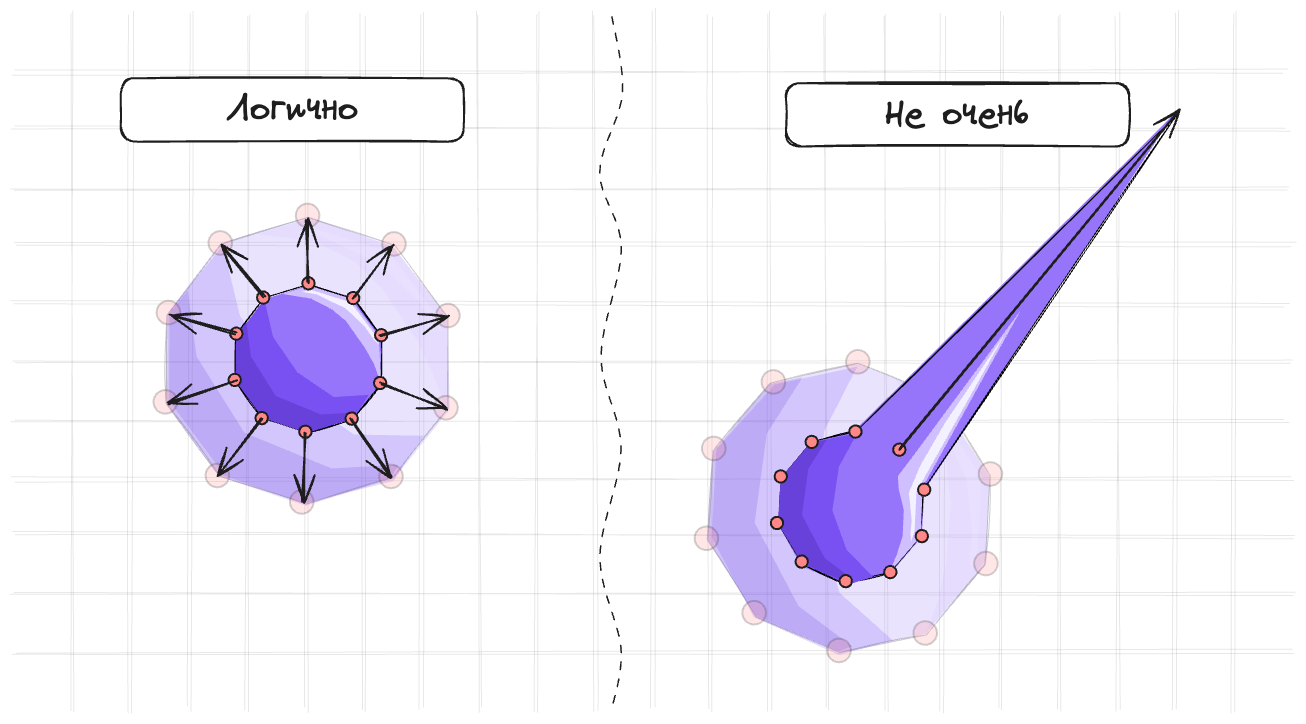
Собственно вот этот множитель $s$ и позволяет нам делать это. Мы сдвигаем все точки на одинаковое расстояние.

Добавляем массу

Как и в прошлом методе, хочется, чтобы точка потяжелее двигалась меньше при разрешении ограничения. Дальше тк мы постоянно делим на массу в уравнениях очень часто будет встречаться понятие инвертированной массы. $w = \frac{1}{m}$. Инвертированной массой очень просто определять несдвигаемые точки – точку с бесконечной массой. Для нее $w = 0$.

Для того чтобы учесть инвертированную массу прошлое уравнение $\Delta \vec{p} = \lambda \nabla_p C(\vec{p})$ скалируют на инвертированную массу и получают вот такое уравнение: $\Delta \vec{p} = -s * \nabla_{\vec{p_i}} C * w_i$

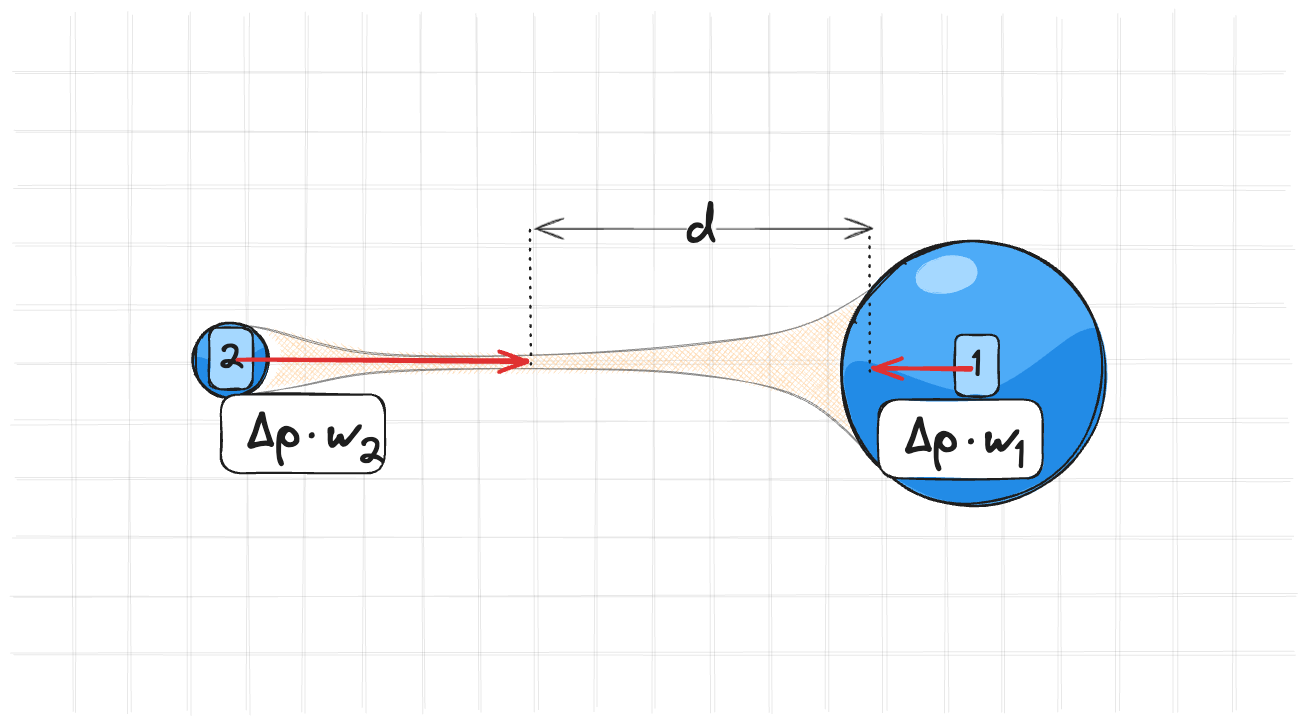
Если его разрешить, то получится вот такие уравнения:

$$ \begin{equation} \begin{split} &\Delta \vec{p_i} = -s * w_i * \nabla_{\vec{p_i}} C \\ &s = \frac{C}{\sum_{k} (w_k * \nabla_{\vec{p_k}} C)^2} \end{split} \end{equation} $$

Обратите внимание, что теперь в знаменателе стоит $w_k * \nabla_{\vec{p_k}} C$.

Вот собственно и рецепт разрешения ограничений в PBD.

Неравенства

Ограничения могут быть в виде неравенств. Как и в прошлом методе. Их переводят в ограничение равенства и разрешают его только если оно нарушено.

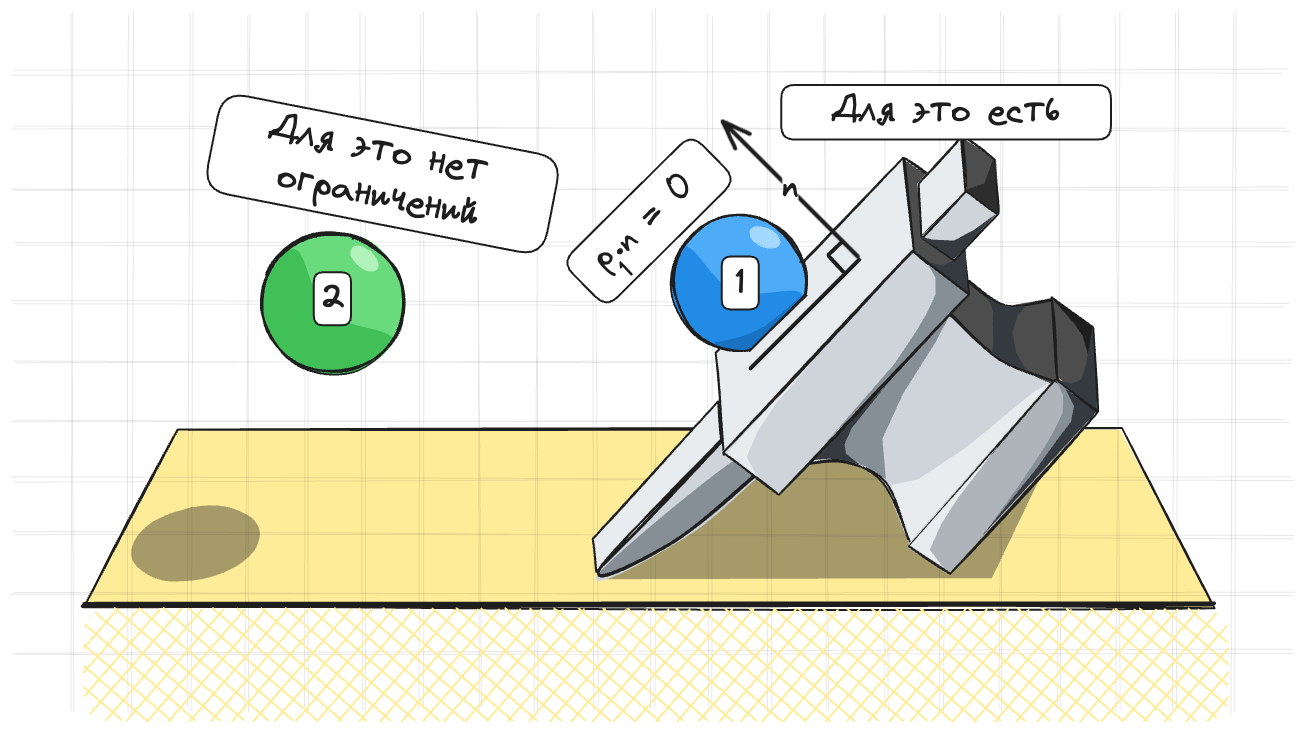
Например коллизия для точки со статическим объектом описывается вот таким ограничением:

$$ C(\vec{p_1}) = (\vec{p_1} - \vec{q_s})\cdot \vec{n} \leq 0 $$

И разрешать мы будем только если оно уже нарушилось в виде

$$ \begin{equation} C(\vec{p_1}) = (\vec{p_1} - \vec{q_s})\cdot \vec{n} = 0 \end{equation} $$

Коллизии

Коллизии в PBD разрешаются в несколько этапов.

Первый этап – поиск коллизий.
Второй этап – разрешение коллизий по позициям.
Третий этап – разрешение коллизий по скоростям (трение и упругость)

Поиск коллизий

Тк алгоритм поиска коллизий достаточно медленный, то он запускается один раз перед разрешением всех ограничений. Это приводит к тому, что при разрешении всех ограничений, может возникнуть новая коллизия.

Вот например ситуация

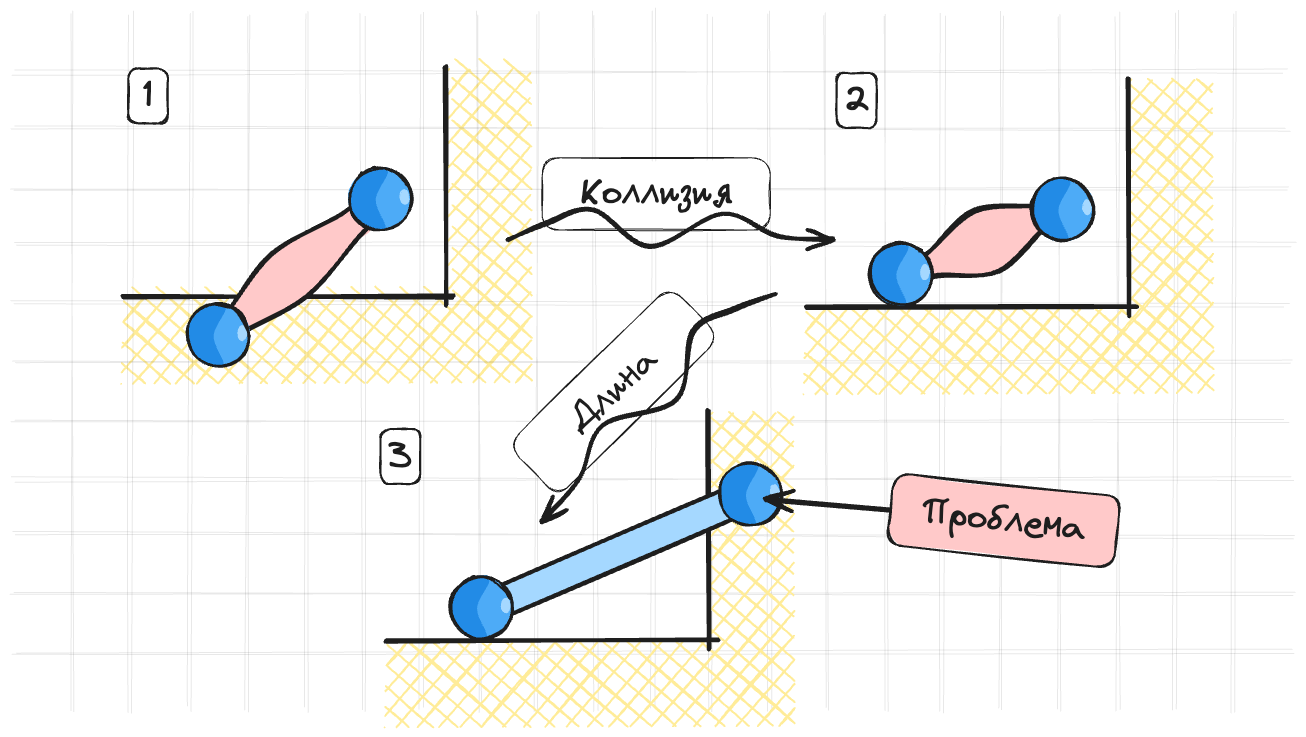
Палочка врезается в стену. Мы фиксируем коллизию. И разрешаем ее. Потом мы восстанавливаем длину палочки и после этого другая точка палочки врезается в стену.

Авторы никак не решают эту проблему. На практике она не сильно заметна для пользователя, тк на следующей итерации физика все равно исправит эту коллизию.

Разрешение коллизий по позициям

Статические объекты

Для статических объектов разрешение коллизий выглядит просто. Нужно просто выдавить точку из объекта в правильную полуплоскость. Как уже говорил выше, это делается вот таким ограничением:

Для этого в при инициализации коллизионной информации нужно определить $\vec{n_s} – нормаль и $\vec{q_s} – проекцию точки на поверхность.

После этого в релаксации требовать чтобы выполнялось ограничение:

$$ \begin{equation} C(\vec{p_1}) = (\vec{p_1} - \vec{q_s}) \cdot \vec{n_s} = 0 \end{equation} $$

Я заметил, что в релаксации лучше делать проверку на нарушение коллизии в виде неравенства. Т.е если $C(\vec{p_1}) < 0$, то нужно разрешить коллизию. Тк чистое равенство создает ощущение “прилипания к стенке”.

Динамические объекты

Теперь нужно разобраться как разрешать коллизии между двумя динамическими объектами.

Сначала в 2D. Вот шарик летит в систему шариков.

Если он попал в связь между шариками, то наша задача выдавить шарик в правильную полуплоскости.

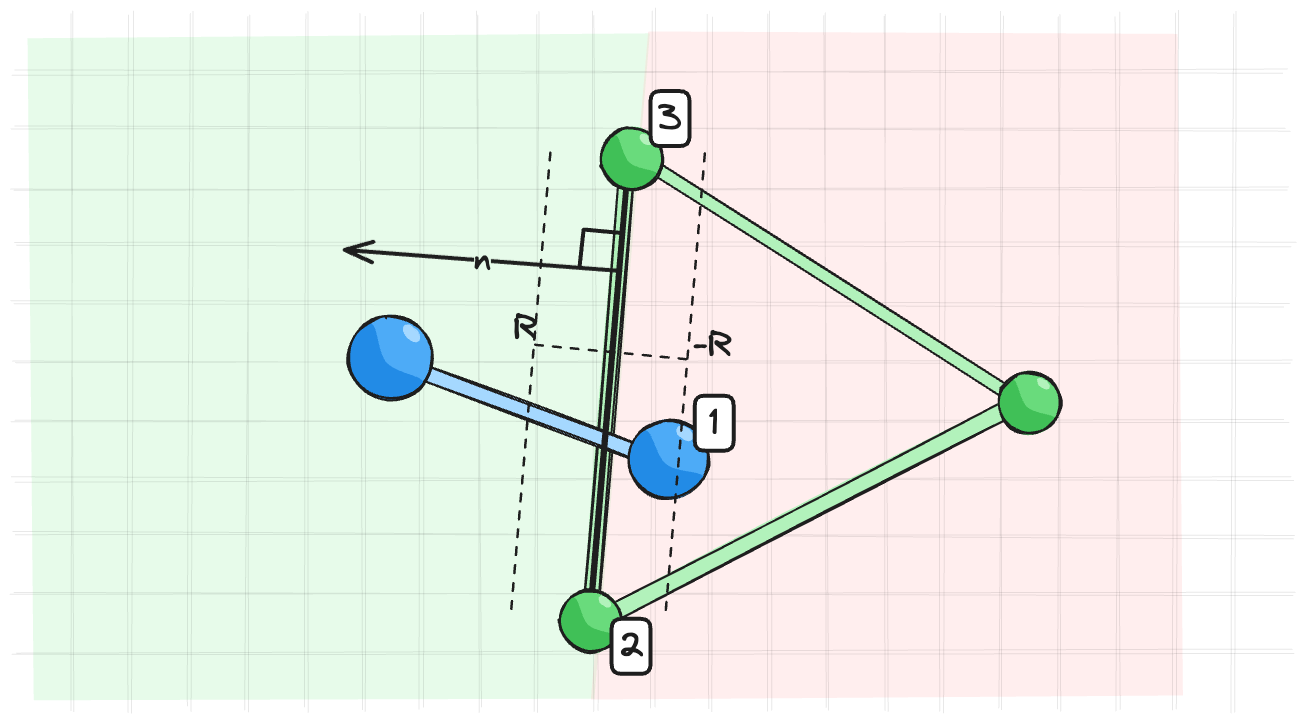
Ограничение коллизии между шариком $\vec{p_1}$ и линией образованной двумя другими шариками $\vec{p_2}$ и $\vec{p_3}$ можно описать вот так:

$$ \begin{equation} \begin{split} &\vec{m_p} = \vec{p_1} + \frac{(\vec{p_2} - \vec{p_1}) \cdot (\vec{p_3} - \vec{p_1})}{||\vec{p_2} - \vec{p_1}||^2} \cdot (\vec{p_2} - \vec{p_1}) \\ &\vec{d} = \vec{m_p} - \vec{p_1} \\ &C(\vec{p_1}, \vec{p_2}, \vec{p_3}) = ||\vec{d}|| = 0 \end{split} \end{equation} $$

Это просто расстояние от точки до прямой. Если есть какой-то радиус у точки, то нужно учитывать полуплоскость в которую нужно выдавить точку. От этого зависит знак в ограничении.

$$ \begin{equation} C(\vec{p_1}, \vec{p_2}, \vec{p_3}) = \pm ||\vec{d}|| - R = 0 \end{equation} $$

Теперь в 3d.

Идея та же самая, просто вместо прямой у нас плоскость из трех точек.

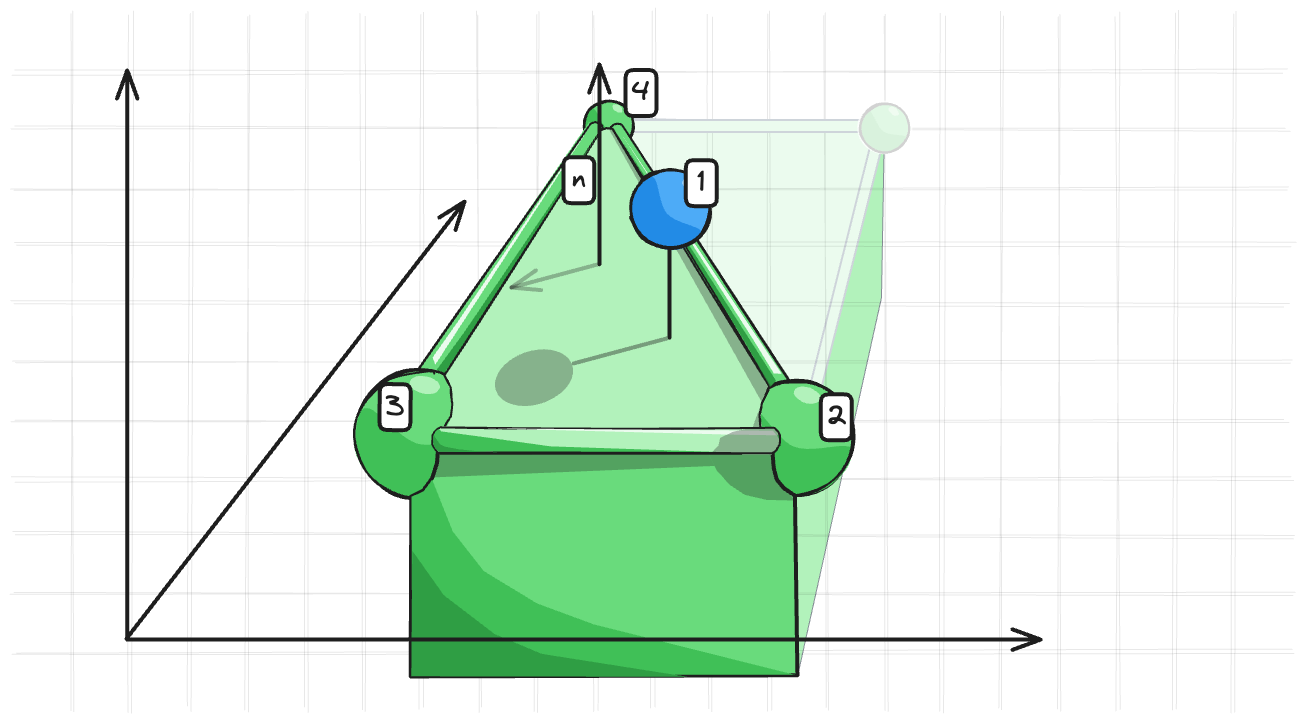
Мы должны держать точку 1 на расстоянии $R$ от плоскости образованной точками 2, 3 и 4. Ограничение будет вот таким:

$$ \begin{equation} \begin{split} &\vec{n} = [(\vec{p_3} − \vec{p_2}) \times (\vec{p_4} − \vec{p_2})] \\ &C(\vec{p_1},\vec{p_2},\vec{p_3},\vec{p_4}) = \pm (\vec{p_1}−\vec{p_2}) \cdot \vec{n} - R = 0 \end{split} \end{equation} $$

Трение и упругость

Для того чтобы было ощущение столкновения, нужно правильно изменить скорости точек.

Тк у нас есть скорости в явном виде, это достаточно просто сделать. Для ощущения трения уменьшаем тангенциальную скорость. Для упругости отражаем нормальную скорость.

И вот мы наконец-то можем реализовать нормальное мягкое тело с трением и упругостью.

Дампинг скорости

В этой статье предложен дампинг скорости, который позволяет сделать условно твердые тела более твердыми. Т.е если у нс есть фигура из материальных точек и мы соединяем их пружинками, то при движении фигура будет деформироваться, тк не все ограничения на длину успеют разрешиться. Для того чтобы сделать тело более твердым, предлагается добавить особенный дампинг скорости.

Псевдокод дампинга скорости

dampVelocity(points) {
    // Находим центр масс
    x_center_of_mass = vec(0);
    // скорость центра масс
    v_center_of_mass =  vec(0);
    for (let point of points) {
        x_center_of_mass += point.x;
        v_center_of_mass += point.v;
    }
    x_center_of_mass /= points.length;
    v_center_of_mass /= points.length;

    // Угловой момент
    angular_momentum = vec(0);
    // Момент инерции
    Inertia = mat(0);
    for (let point of points) {
        let r = point.x - x_center_of_mass;
        let r_t = point.v - v_center_of_mass;
        angular_momentum += r.cross(r_t);
        Inertia += r.cross(r);
    }
    // Расчитываем угловую скорость
    let omega = Inertia.inverse().dot(angular_momentum);
    // Дампинг скорости деформации
    for (let point of points) {
        let r = point.x - x_center_of_mass;
        let r_t = point.v - v_center_of_mass;
        let delta_v = v_center_of_mass + omega.cross(r) - point.v;
        point.v += damping * delta_v;
    }
}

Скорость точки представляется как сумма скорости центра масс, угловой скорости и скорости деформации. И демпингуется только скорость деформации.

Основная часть закончилась. Остались только разные ограничение и как реализовывать их в PBD.

Разные ограничения

Источники

Оригинальная статья Position Based Dynamics
Хороший видос с объяснением Position Based Dynamics

2. Метод Hitman Codename 47 4. XPBD и SmallSteps