10. Sequential Impulses
Интро
В предыдущих методах мы решали ограничения с помощью манипуляций позиций и поворотов тел. Он отлично работает для симуляции мягких тел, волос, тканей и прочего. Но у этого способа есть недостатки: Склеивание шариков. Плохой отскок. Много итераций.
Поэтому умные ребята придумали другой способ разрешать ограничения.
Основная идея. Вот у нас есть какое-то ограничение зависящее от позиции $$ C(x) = 0 $$
Если продифференцировать это ограничение по времени, то получим скорость точки в направлении ограничения. $$ \dot{C}(x) = \frac{dC}{dx} \cdot \dot{x} $$
Теперь мы можем использовать это уравнение для того чтобы изменить скорость точки так, чтобы она удовлетворяла ограничению. Если мы в каждый момент времени будет выставлять скорость точки правильным образом, то оригинальное ограничение будет удовлетворено.
Пример
Пусть это будет ограничения на дистанцию точки от подвеса. $$ C(x) = |x - x_0|^2 - r^2 = 0 $$
Если продифференцировать это ограничение по времени, то получим скорость точки в направлении ограничения. $$ \dot{C}(x) = 2(x - x_0) \cdot \dot{x} = 0 $$
Для нас это означает, что проекция скорости точки на вектор от точки до подвеса должна быть равна нулю. $$ v_{\parallel} = (x - x_0) \cdot \dot{x} = 0 $$ Или, что скорость точки должна быть перпендикулярна вектору от точки до подвеса.
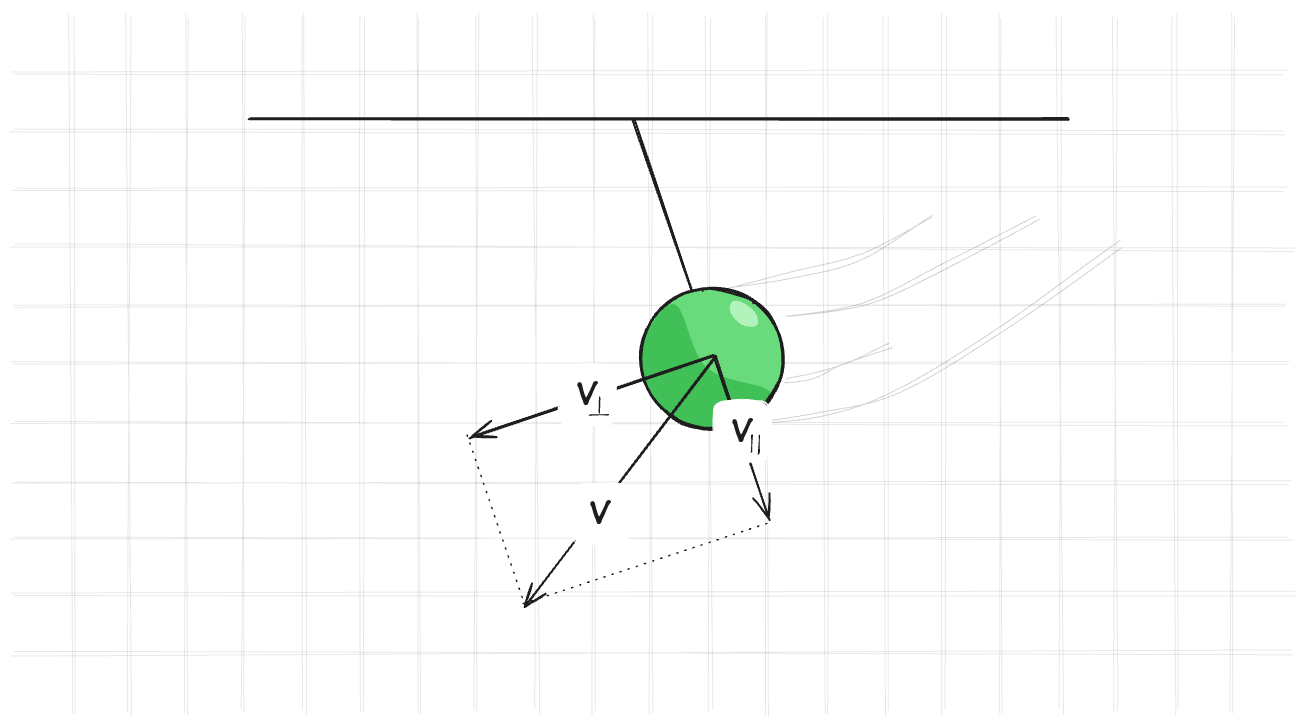
Если скорость всегда будет перпендикулярна вектору от точки до подвеса, то ограничение на дистанцию будет удовлетворено.