1. Уравнение Навье-Стокса

Уравнение Навье-Стокса

Уравнение Навье-Стокса – база почти для всех методов симуляции жидкостей и газов. Оно описывает жидкость как макроскопическую субстанцию, в которой есть скорость, давление и вязкость. Те если мы будем смотреть на очень маленький кусочек жидкости, для нас этот кусочек все равно останется жидкостью, а не молекулами. Такое уравнение описывает жидкость как что-то непрерывное.

Вот такое стремное уравнение: $$ \frac{\partial \mathbf{u}}{\partial t} = - (\mathbf{u} \cdot \nabla) \mathbf{u} -\nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{f} $$

где $\mathbf{u}$ - вектор скорости, $p$ - давление, $\nu$ - вязкость, $\mathbf{f}$ - внешние силы.

$\frac{\partial \mathbf{u}}{\partial t}$ - изменение скорости во времени (обычное ускорение) маленького кусочка жидкости.

Каждую часть справа у уравнения можно интерпретировать:

Pressure

$-\nabla p$

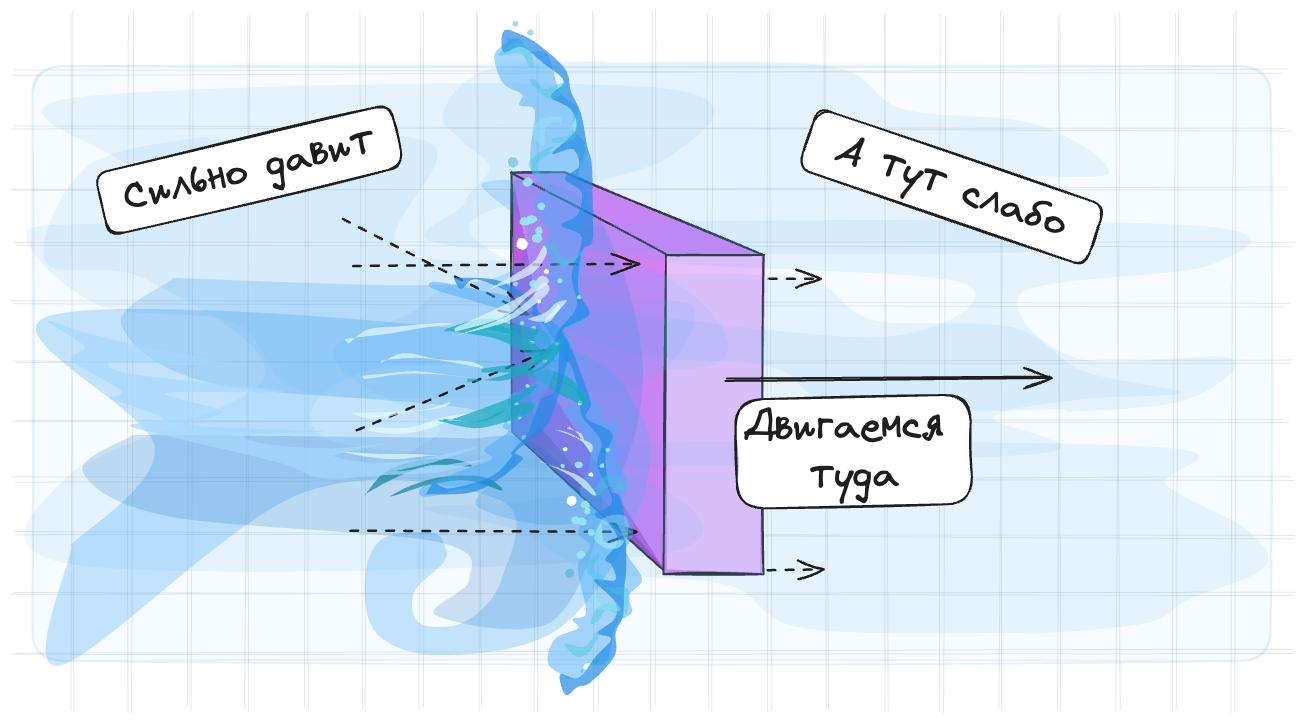
Давление влияет на ускорение. Если в каком-то месте давление больше, чем в другом, то жидкость будет двигаться из места с большим давлением в место с меньшим. Как по мне это самый простой и логичный элемент уравнения – Двигаемся туда где слабее давят.

Advection

$ -(\mathbf{u} \cdot \nabla) \mathbf{u}$

Жидкость переносит свою скорость вместе с собой. Мне это очень сложно представить, поэтому рассмотрим пример с частицами. В жидкости есть ээ черные чернила от осьминога $a$ (Представьте жидкость без диффузии). Или очень вязкую жидкость. У нас есть вот такое уравнение $$ \frac{d \mathbf{a}}{dt} = - \mathbf{u} \cdot \nabla \mathbf{a} $$

В таком контексте понятно, что изменение количества чернил зависит от скорости жидкости. Если жидкость двигается, то чернила тоже двигаются.

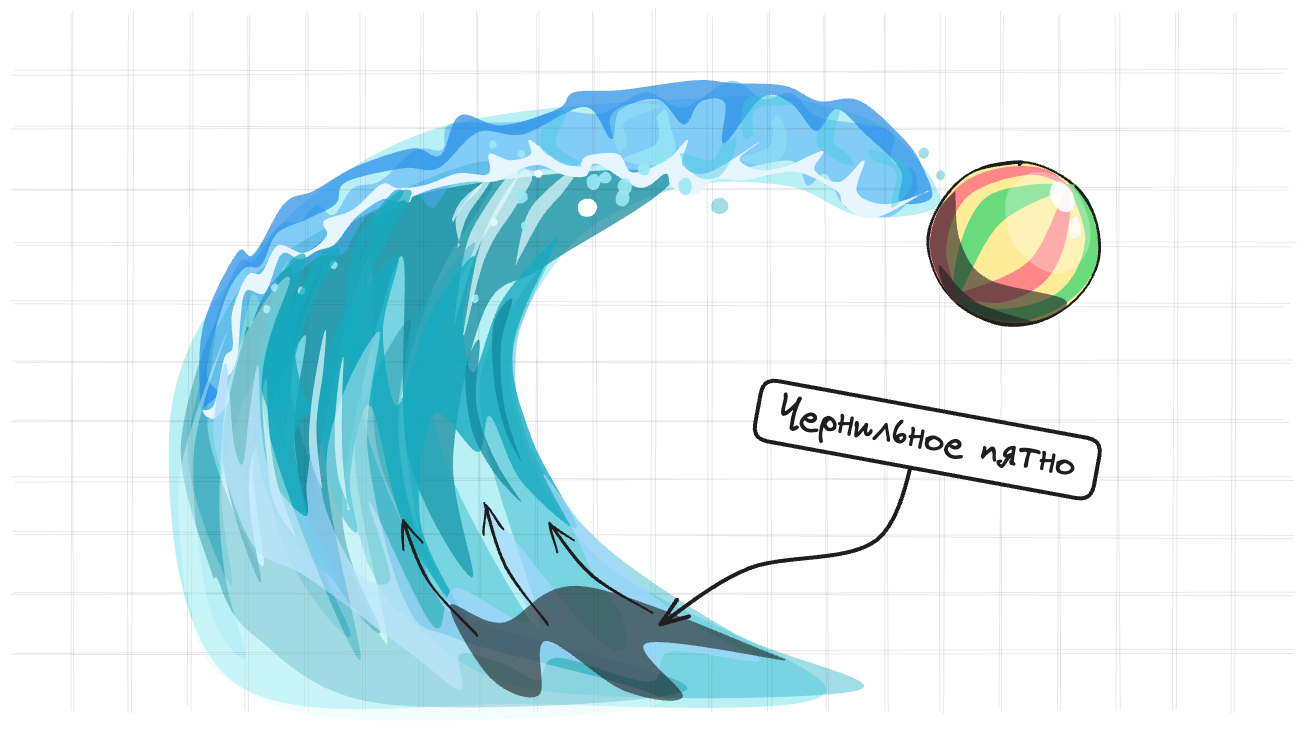
Точно так же происходит и со скоростью жидкости. Она переносится из-за того что жидкость движется.

Viscosity

$\nu \nabla^2 \mathbf{u}$

Молекулы обмениваются скоростями между собой. Из-за этого скорость среды немного сглаживается. Это можно представить, как будто между молекулами есть пружинки, которые обменивают скорость.

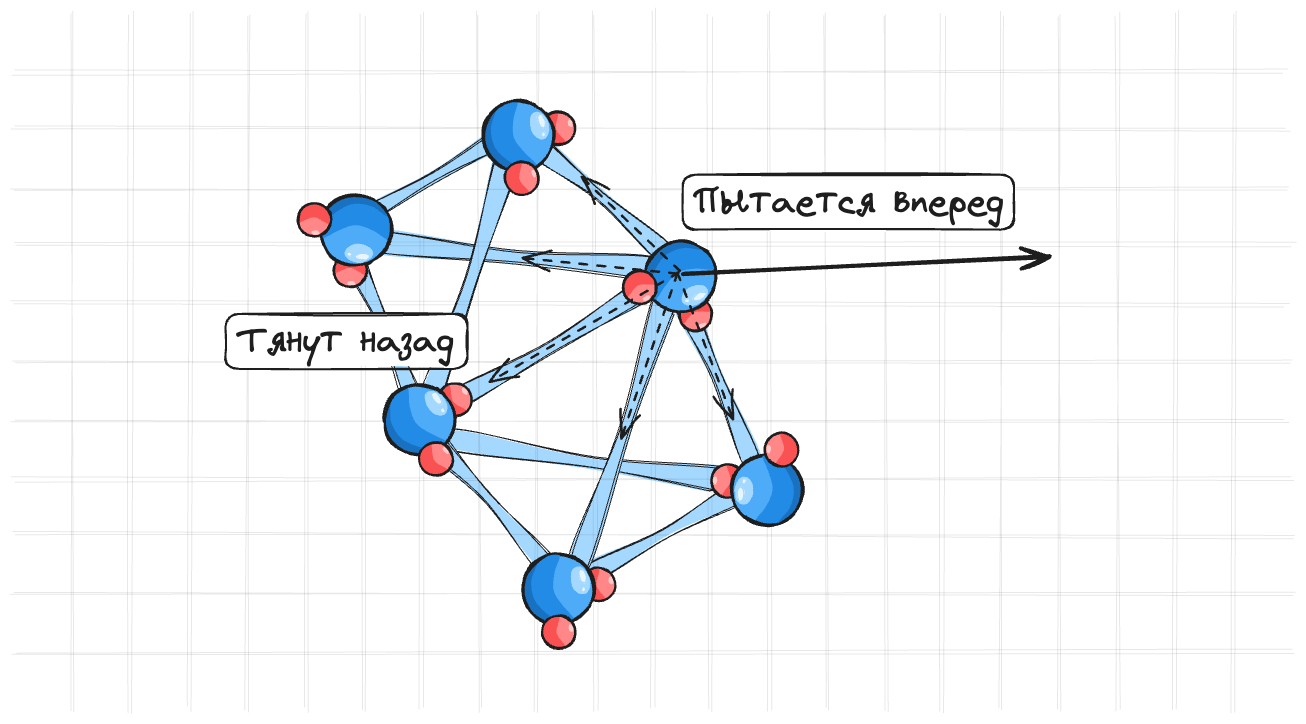
Из-за того что между молекулами жидкости есть взаимодействие, скорость молекулы передается остальным. Если жидкость вязкая, то связи между молекулами сильные и одной молекуле приходится тащить за собой больше молекул.

Забавно, что в газах механизм вязкости другой. Там молекулы сталкиваются друг с другом и передают импульс за счет столкновений.

External forces

$\mathbf{f}$ Внешние силы. Ну тут все понятно, если на нашу жидкость действуют какие-то силы, то она будет двигаться в соответствии с ними. Например, гравитация.

Несжимаемость

Для несжимаемой жидкости уравнение дополняется уравнением ага ага несжимаемости:

$$ \nabla \cdot \mathbf{u} = 0 $$

Это уравнение нарушается при двух условиях либо у нас есть источники или стоки жидкости

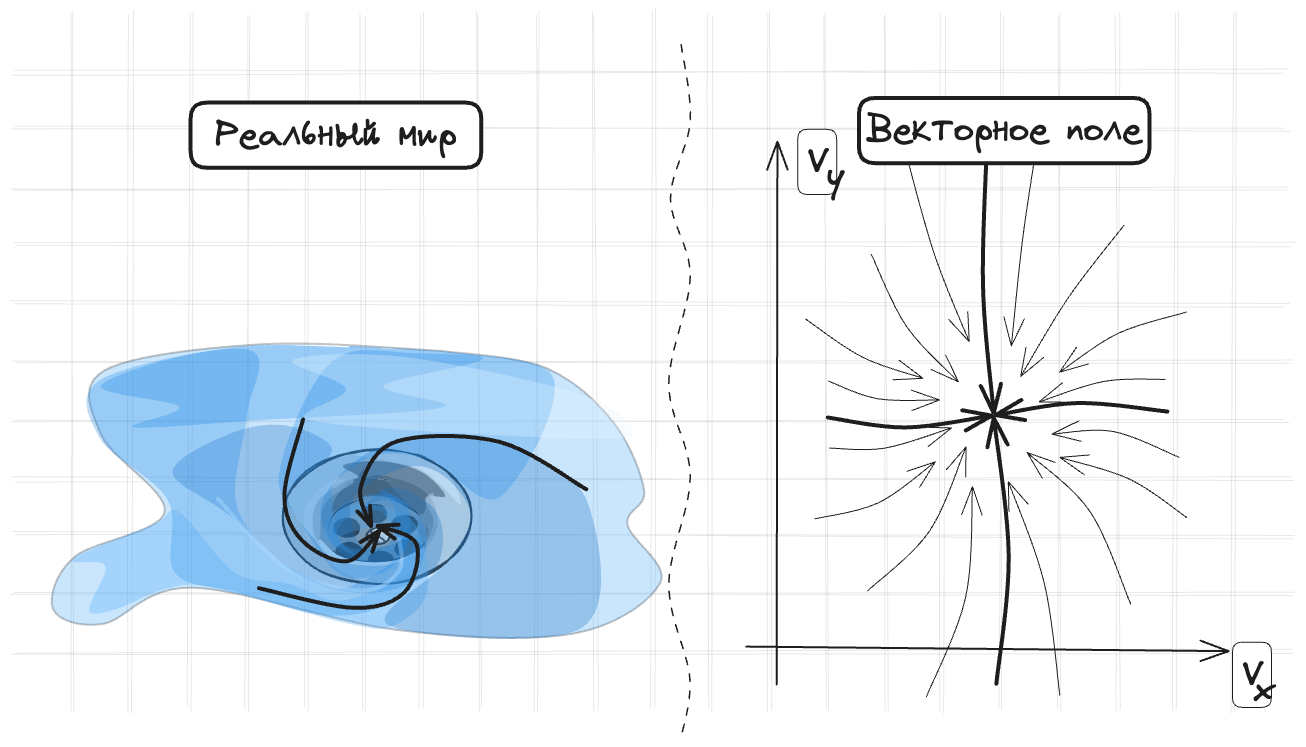
Либо если жидкость сжимаема. Мне представить себе сжимаемую жидкость сложно, со школы говорили, что водичку нельзя сжать и у меня теперь это не получается. Зато получается представить как воздух сжимается в поршне. Тогда скорости будут направлены друг на друга как-то так:

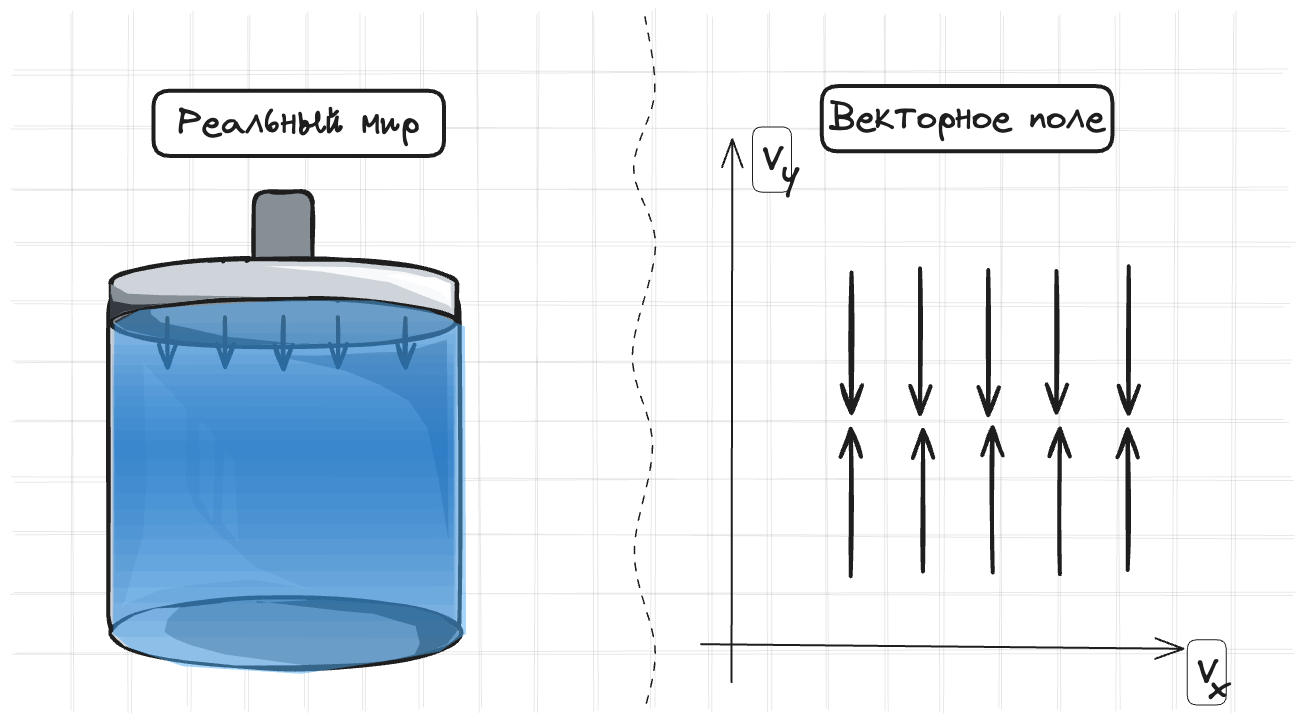
На самом деле, в реальности все жидкости сжимаемы. Но для художественных задач, практика показывает, что этим даже лучше пренебречь. Так получается красивее и проще. Более того часто даже для симуляции газов получается красивее, если считать их несжимаемыми.

Как описывать?

Вот мы определили уравнение, но как его решать? Как минимум нужен инструмент описания среды в которой это все происходит. В реальной жизни есть всякие молекулы и группы, у которых можно определить скорость. В компьютерной графике это все абстрагируется:

Идейно есть два подхода для описания среды:

• Эйлеровый - мы разбиваем пространство на кусочки и в каждом храним нужные параметры, например скорость и давление. Это может быть как просто равномерная сетка по всему пространству, так и что-то более сложное и динамическое.

• Лагранжевый - каждая частица имеет свои параметры, и мы их обновляем

У каждого подхода есть свои минусы и сейчас самые популярные методы – гибридные.