3. Расчет параметров по мешу

Имея на руках меш, можно рассчитать различные параметры: объем, площадь поверхности, центр масс, момент инерции и тому подобное.

Площадь в 2D

Есть фигура в 2D заданная точками. Точки упорядочены по часовой стрелке. Нужно найти площадь фигуры.

Для этого есть отличный алгоритм - формула площади Гаусса или (Shoelace_formula)[https://en.wikipedia.org/wiki/Shoelace_formula]

Идея очень простая. Мы легко можем посчитать площадь треугольника, если знаем координаты его вершин. Еще легче посчитать если одна из вершин находится в начале координат.

Если у нас есть треугольник с вершинами $(x_1, y_1), (x_2, y_2), (0, 0)$. Тогда площадь треугольника равна:

$$ S = \frac{1}{2} \left| x_1 y_2 - x_2 y_1 \right| $$

Эта формула дает положительное значение, если вершины заданы по часовой стрелке и отрицательное, если против часовой стрелки. И если проссумировать площади всех треугольников, образованных вершинами последовательных точек, то мы получим площадь фигуры.

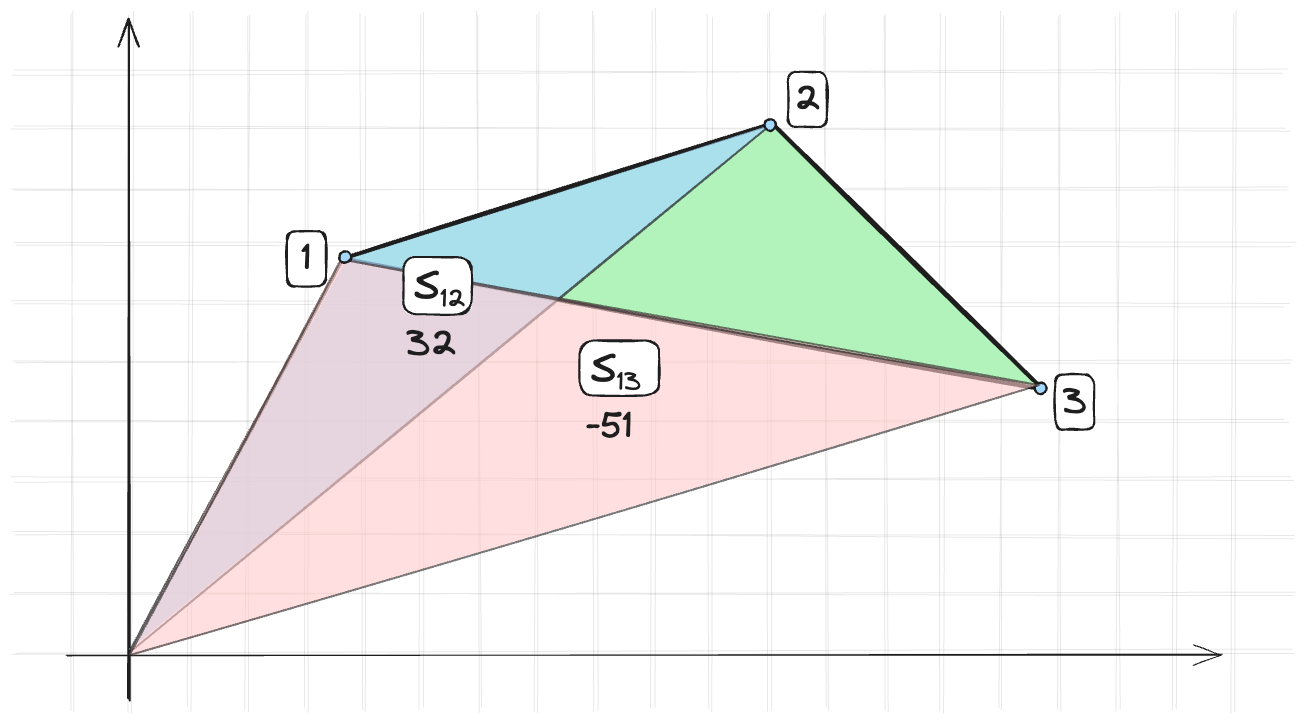
Обобщая, площадь фигуры равна: Пусть у нас есть фигура заданная точками $(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)$. Тогда площадь фигуры равна:

$$ S = \frac{1}{2} \left| \sum_{i=1}^{n-1} x_i y_{i+1} + x_n y_1 - y_i x_{i+1} - y_n x_1 \right| $$