1. Численные методы
Интро
То ли мы глупые, то ли вселенная такая несовершенная, но многие дифференциальные уравнения невозможно решить аналитически. Например, меня удивляет, что задача трех тел уже неразрешима. С другой стороны, если бы такие траектории можно было описать аналитически, это было бы очень круто. Вы только взгляните, какая красота:
В играх приходится иметь дело с системами гораздо сложнее, чем взаимодействие трех тел, которые тоже вряд ли получится решить аналитически. Поэтому много умных людей разработали численные методы. Базовая идея такова: имея начальную точку, получаем лишь одно решение, в то время как аналитический метод дает все решения. Но в большинстве случаев нам нужно только одно. В игре уже есть начальное состояние, и мы просто хотим узнать, что будет дальше.
Стоит сказать, что все счастливые семьи, в которых все уравнения решаются аналитически, похожи друг на друга. Они просто подставляют в решение время и получают все, что нужно. Несчастливая семья же несчастна по-своему. Разным играм нужны разные свойства от физических движков. разработчики симулируют только частицы, другие — только твердые тела. Кому-то очень важна точность, а кому-то нужно, чтобы просто было стабильно и хоть немного похоже на правду. Тут нет правильного рецепта и каждый страдает в меру своих ограничений.
Здесь я попробую рассказать о самых популярных и используемых методах численного интегрирования.
Необходимые знания
Фазовое пространство
Помимо основных знаний о дифференциальных уравнениях, для понимания дальнейшего материала нужно знать, что такое фазовое пространство. Формальное определение:
<p>“Фазовое пространство — это пространство четной размерности, координатами в котором являются обычные пространственные координаты (или обобщённые координаты) частиц системы и их импульсы.”</p>
Нам же достаточно понимать малую часть от этого. Для одномерной системы, например, пружины, которая может колебаться по одной оси, фазовое пространство — это график, где на одной оси у нас координата, а на другой — импульс. Точка на этом графике — это состояние системы.
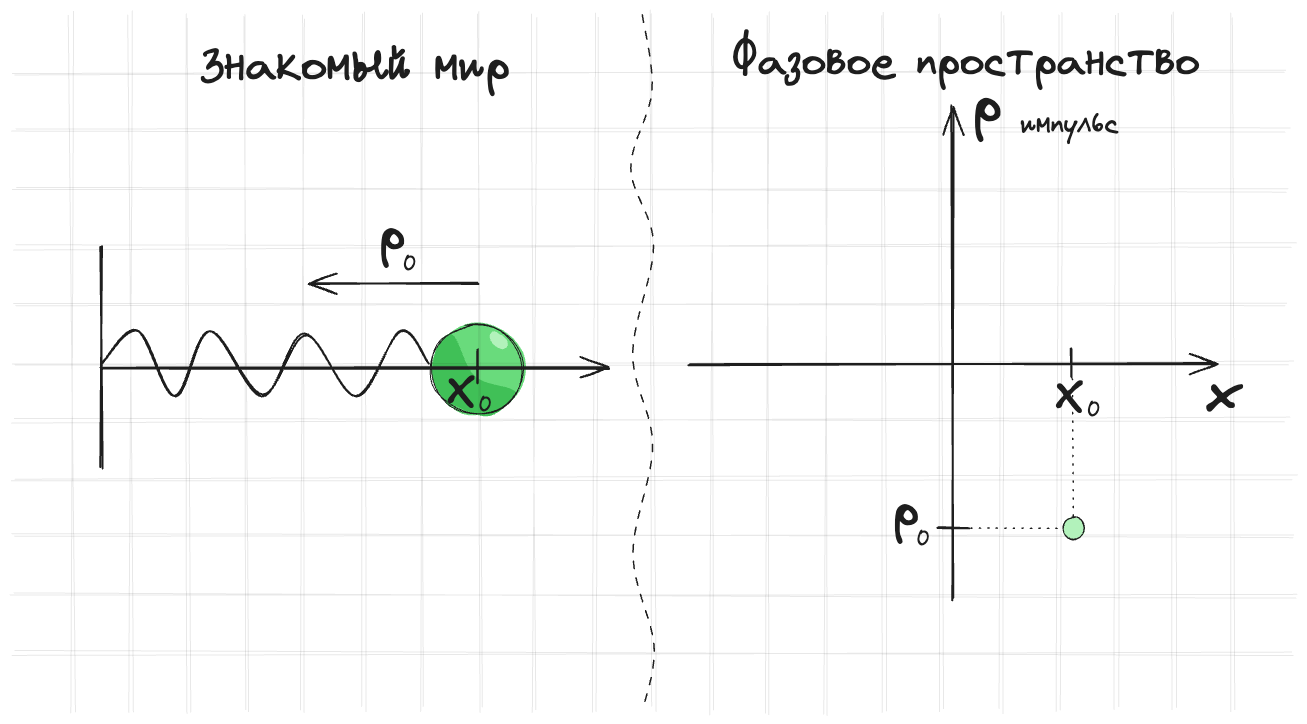
Если же пружинка может колебаться в двух направлениях, то фазовое пространство будет четырехмерным — импульсы и координаты по двум направлениям.
Векторные поля
Очень полезно и приятно рисовать векторные поля системы на фазовом пространстве. Векторное поле — это набор векторов, каждый из которых показывает направление и скорость изменения в каждой точке фазового пространства. Вот так будет выглядеть фазовое пространство для пружинки:
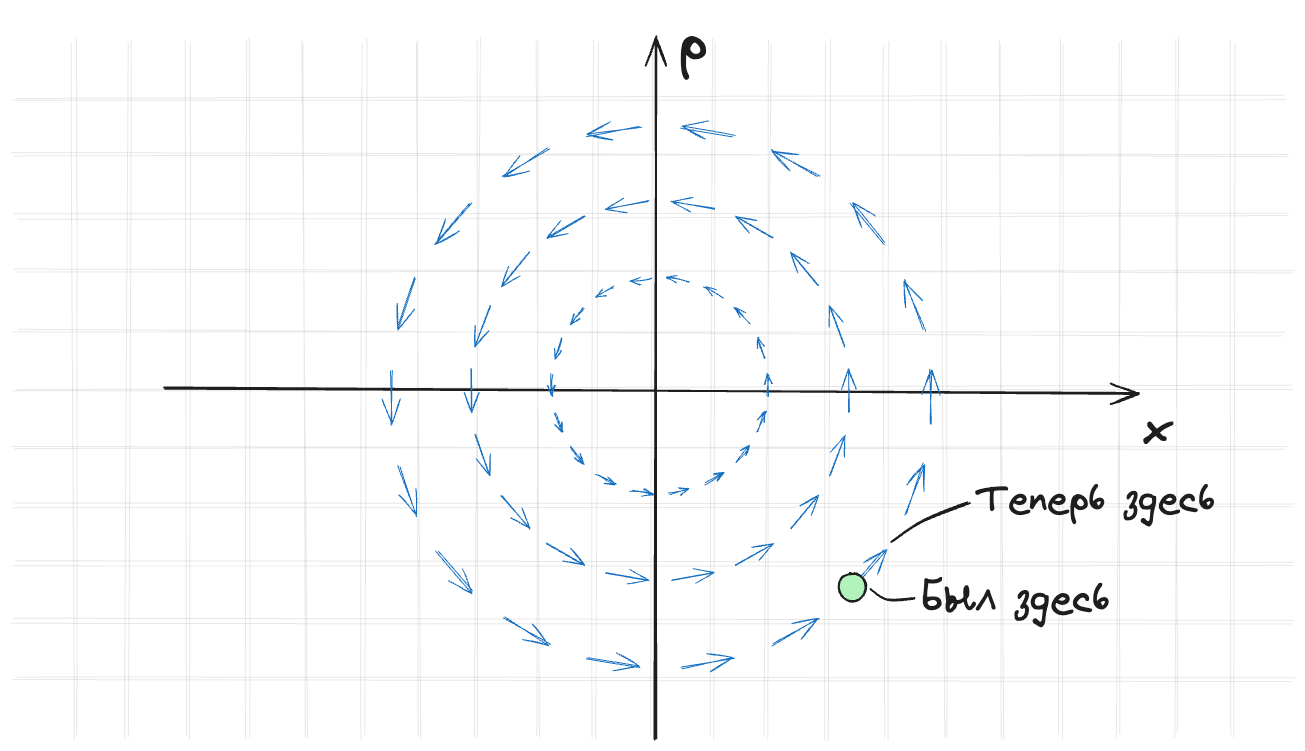
Модельные задача
Для анализа численных методов возьмем простые задачи, которые достаточно часто встречаются в играх и для которых известно аналитическое решение.
Возьмем две задачи: Стрельба из пушки и колебания пружинки. Обе задачи очень типичны для физ движка. И хороши тем, что илюстрируют разные типы движения: баллистическое и гармоническое.
Стрельба из пушки
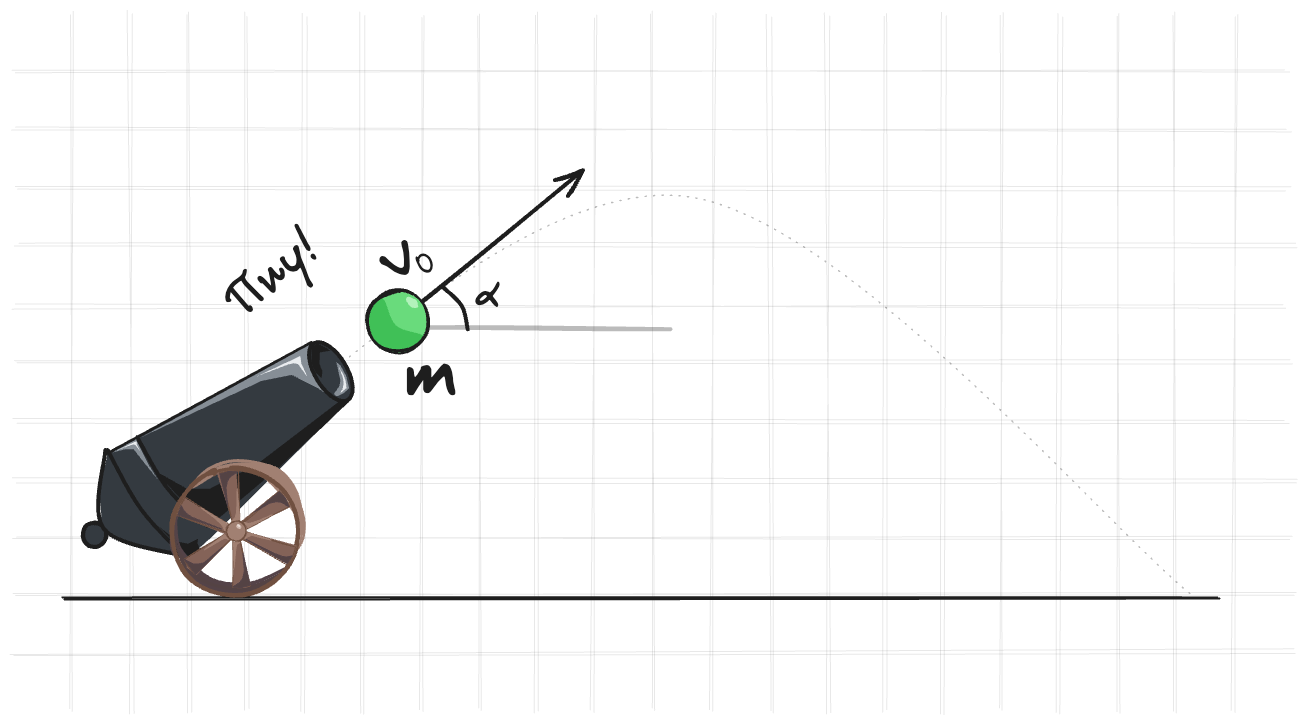
Тело массой $m$ вылетает из пушки с начальной скоростью $v_0$ под углом $\alpha$ к горизонту. Тогда уравнение движения примет вид $$
\begin{equation*}
\begin{split}
\ddot{x} = 0,\\
\ddot{y} = -g,
\end{split}
\end{equation*}
$$ где $g$ - ускорение свободного падения. Перепишем уравнение в виде
$$
\begin{equation*}
\begin{split}
&\dot{x} = v_x,\\
&\dot{v_x} = 0,\\
&\dot{y} = v_y,\\
&\dot{v_y} = -g.
\end{split}
\end{equation*}
$$
Если ввести вектор состояния $z$:
$$
\begin{equation*}
z =
\begin{bmatrix} x \\ v_x \\ y \\ v_y \\ \end{bmatrix}
\end{equation*}
$$
и константный вектор $G$:
$$
\begin{equation*}
G = \begin{bmatrix} 0 \\ 0 \\ 0\\ -g \end{bmatrix}
\end{equation*}
$$
Тогда уравнение перепишем в виде
$$
\begin{equation*}
\dot{z} =
\begin{bmatrix}
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
\end{bmatrix}
\cdot z + \begin{bmatrix} 0 \\ 0 \\ 0\\ -g \end{bmatrix} = A \cdot z + G
\end{equation*}
$$Аналитическое решение
Аналитическое решение этой задачи – обычная баллистическая кривая. $$ \begin{equation} \begin{split} &x(t) = v_0 t \cos(\alpha) \\ &y(t) = v_0 t \sin(\alpha) - \frac{1}{2}gt^2. \end{split} \end{equation} $$
Пружинка
Пружинка с коэффициентом жесткости $k$, массой $m$ и начальным смещением $x_0$ и начальной скоростью $v_0$.
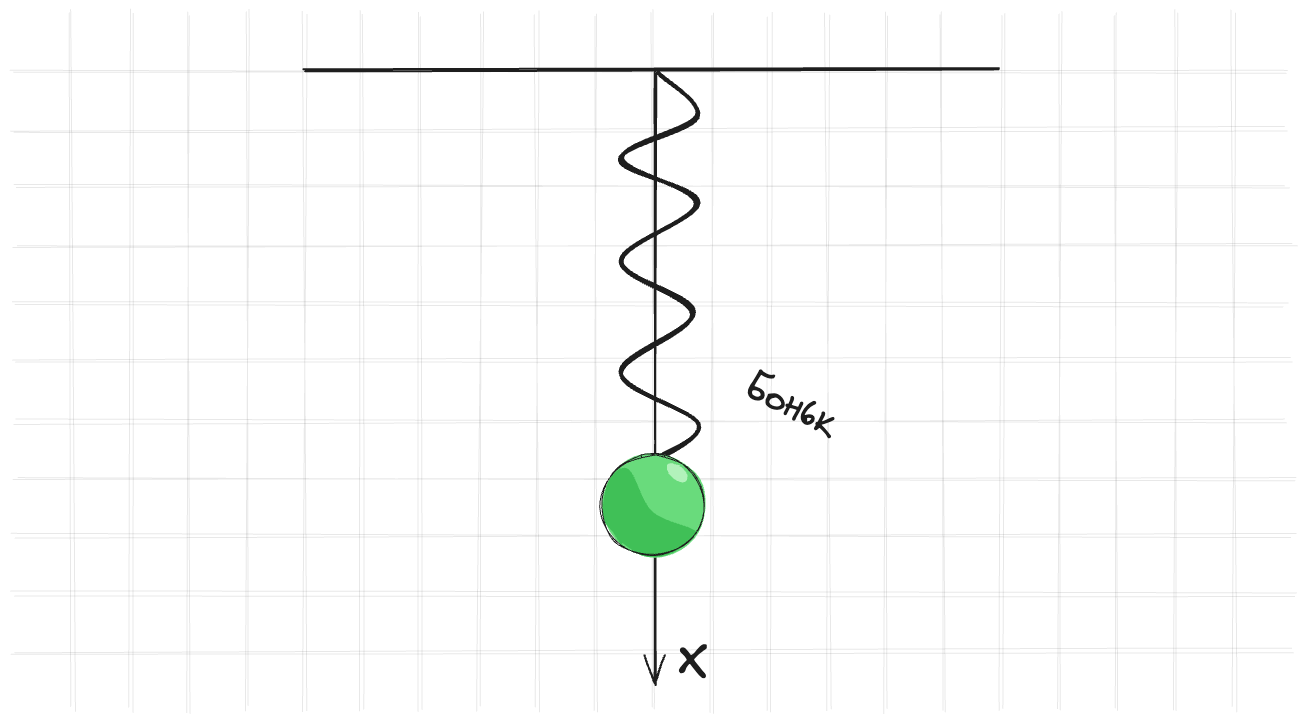
Аналитическое решение
Аналитическое решение для этой задачи – гармонические колебания. $$ \begin{equation} x(t) = (x_0\cos(\omega t) + v_0\sin(\omega t)), \end{equation} $$