1. Прямой и Обратный методы Эйлера
Прямой метод Эйлера
Самый простой метод численного интегрирования можно получить, если заменить в определении производной приближение на равенство: $$ \begin{equation} \dot{x} = \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0} \frac{x(t + \Delta t) -x(t)}{\Delta t} \approx \frac{x(t + \Delta t) -x(t)}{\Delta t}, \end{equation} $$
$$ \begin{equation} x(t + \Delta t) = x(t) + \dot{x}(t)\Delta t \end{equation} $$ Или в дискретной форме $$ \begin{equation} x_{k+1} = x_k + \dot{x_k}\Delta t \end{equation} $$ Этот метод был предложен более 200 лет назад и называется методом явного Эйлера (Explicit Euler). Такие схемы называются явными, так как, зная $x_k$, можно вычислить $f(x_k)$ и посчитать $x_{k+1}$.
Пока забъем на анализ устойчивости и точности и просто попробуем просимулировать решения модельных задач.
Пушка прямым методом Эйлера
Решение стрельбы прямым Эйлером
$$ \dot{z} = A \cdot z + G $$
Подставляя это в метод прямого Эйлера получим $$ \begin{equation*} \begin{split} &z_{k+1} = z_k + A\cdot z_k\cdot\Delta t + G\cdot\Delta t = \\ &= (I + A\cdot\Delta t)\cdot z_k + G\cdot\Delta t = F\cdot z_k + G\cdot\Delta t \\ &z_{k+1} = F\cdot z_k + G\cdot\Delta t \end{split} \end{equation*} $$
Результат неплохой, но ошибка накапливается, и движение начинает отклоняться от аналитического решения.
Пружинка прямым методом Эйлера
Решение пружинки прямым Эйлером
$$ \dot{z} = A \cdot z $$
Подставляя это в метод прямого Эйлера получим $$ \begin{equation*} \begin{split} &z_{k+1} = z_k + A\cdot z_k\cdot\Delta t = (I + A\cdot\Delta t)\cdot z_k = F\cdot z_k\qquad \\ &z_{k+1} = F\cdot z_k \end{split} \end{equation*} $$
Здесь уже видно возрастание энергии, что не является желательным. Уменьшение шага по времени лишь частично решает проблему — энергия все равно будет расти, но медленнее.
Теперь давайте сделаем анализ устойчивости и точности метода Эйлера.
Анализ устойчивости
Формальности
Идея такая $$ \begin{equation*} \begin{split} &x_{1} = F \cdot x_0 \\ &x_{2} = F \cdot x_1 = F^2 \cdot x_0 \\ &\ldots \\ &x_{k} = F^k \cdot x_0 \end{split} \end{equation*} $$
Мы просто возводим матрицу в степень и умножаем на начальное состояние. Если свести задачу к одномерной, то получим: $$ x_{k+1} = \lambda x_k $$
Для устойчивости решения необходимо:
$$ |\lambda| < 1 $$
Для устойчивости многомерной системы необходимо, чтобы все собственные значения матрицы $F$ были меньше 1 по модулю. Для метода Эйлера зона устойчивости выглядит так:
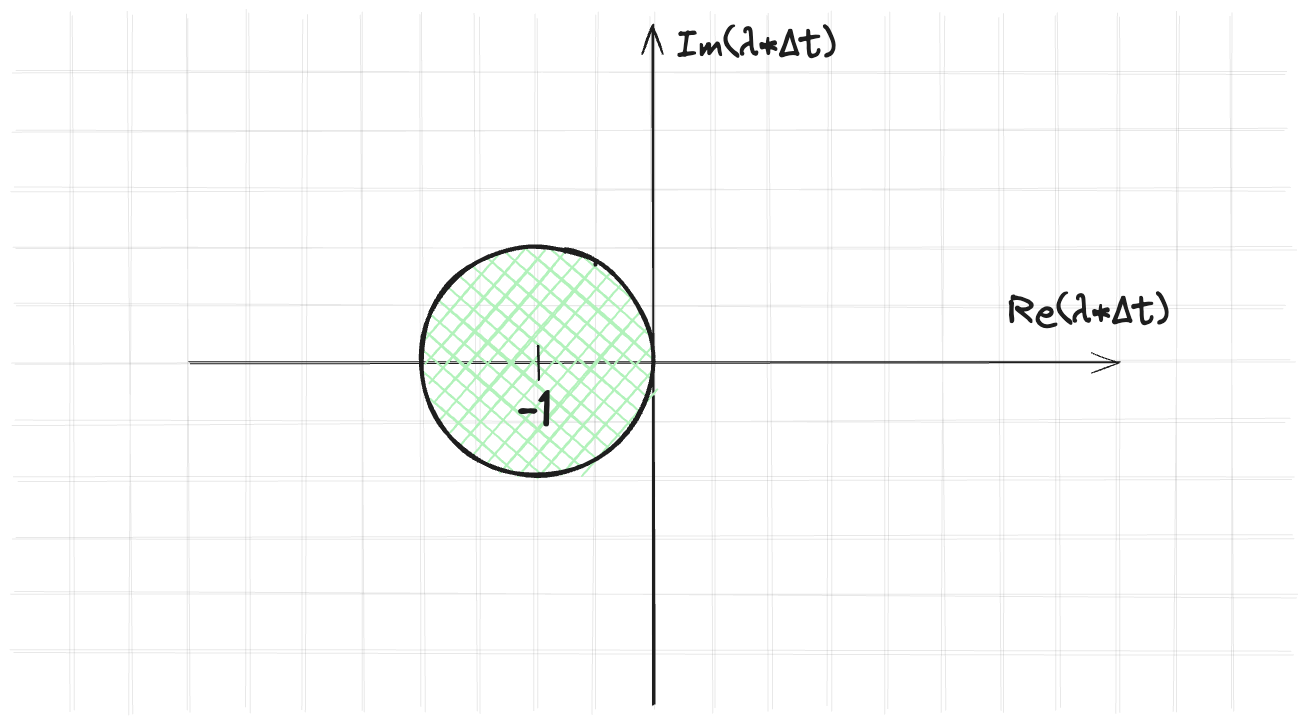
Самое забавное в этом методе, что вот такая недемпфировання пружинка безусловно неустойчива. Те можно уменьшать шаг по времени сколько угодно, но она все равно будет накачиваться энергией и улетать в космос.
Почему в прямом методе Эйлера энергия растет
Рассмотрим уравнение гармонического осциллятора, описывающее движение пружины:
$$ \ddot{x} = -\frac{k}{m}x $$
Перепишем его в виде системы уравнений первого порядка:
$$ \begin{equation*} \begin{split} &\dot{x} = v \\ &\dot{v} = -\frac{k}{m}x \end{split} \end{equation*} $$
Используя метод прямого Эйлера, получаем следующую дискретную форму:
$$ \begin{equation*} \begin{split} &x_{k+1} = x_k + v_k \Delta t \\ &v_{k+1} = v_k - \frac{k}{m}x_k \Delta t \end{split} \end{equation*} $$
Теперь определим полную энергию системы, состоящую из кинетической и потенциальной энергии:
$$ E = T + U = \frac{1}{2}mv^2 + \frac{1}{2}kx^2 $$
Подставим выражения для (x_{k+1}) и (v_{k+1}) и посмотрим, как изменяется энергия:
$$ E_{k+1} = \frac{1}{2}mv_{k+1}^2 + \frac{1}{2}kx_{k+1}^2 $$
Рассчитаем энергию на шаге (k+1):
$$ E_{k+1} = \frac{1}{2}m\left(v_k - \frac{k}{m}x_k \Delta t\right)^2 + \frac{1}{2}k\left(x_k + v_k \Delta t\right)^2 $$
Раскроем скобки и упростим:
$$ E_{k+1} = \frac{1}{2}m \left( v_k^2 - 2\frac{k}{m}v_k x_k \Delta t + \frac{k^2}{m^2}x_k^2 \Delta t^2 \right) + \frac{1}{2}k \left( x_k^2 + 2x_k v_k \Delta t + v_k^2 \Delta t^2 \right) $$
Соберем все слагаемые:
$$ E_{k+1} = \frac{1}{2}mv_k^2 - \frac{k}{m}mv_k x_k \Delta t + \frac{1}{2}k x_k^2 + \frac{1}{2}k v_k^2 \Delta t^2 + \frac{k}{2}x_k v_k \Delta t + \frac{k}{2}v_k^2 \Delta t^2 $$
Сгруппируем похожие слагаемые:
$$ E_{k+1} = \frac{1}{2}mv_k^2 + \frac{1}{2}k x_k^2 + \left( \frac{1}{2}k v_k^2 \Delta t^2 + \frac{1}{2}k x_k v_k \Delta t - \frac{k}{m}mv_k x_k \Delta t \right) $$
Мы видим, что при малых (\Delta t) дополнительные слагаемые не компенсируют начальную энергию, и общий вклад в энергию будет положительным, что приводит к ее возрастанию на каждом шаге:
$$ \Delta E = E_{k+1} - E_k = \left( \frac{1}{2}k v_k^2 \Delta t^2 + \frac{1}{2}k x_k v_k \Delta t - \frac{k}{m}mv_k x_k \Delta t \right) > 0 $$
Таким образом, метод прямого Эйлера приводит к накоплению энергии в системе, что делает его неустойчивым для задач, требующих сохранения энергии, таких как симуляция гармонических осцилляторов.
Анализ точности
Локальная ошибка метода Эйлера – это ошибка, возникающая на каждом шаге интегрирования.
Глобальная ошибка – это накопленная ошибка после $(N)$ шагов интегрирования.
Ошибка метода Эйлера
Рассмотрим функцию (x(t)) и её разложение в ряд Тейлора:
$$ x(t + \Delta t) = x(t) + \dot{x}(t)\Delta t + \frac{\ddot{x}(t)\Delta t^2}{2} + O(\Delta t^3) $$
Метод прямого Эйлера аппроксимирует это разложение следующим образом:
$$ x_{k+1} = x_k + \dot{x}_k \Delta t $$
Локальная ошибка на каждом шаге определяется как разница между точным решением и аппроксимацией методом Эйлера:
$$ e_{\text{local}} = x(t + \Delta t) - x_{k+1} $$
Подставим аппроксимацию и разложение в ряд Тейлора:
$$ e_{\text{local}} = \left(x(t) + \dot{x}(t)\Delta t + \frac{\ddot{x}(t)\Delta t^2}{2} + O(\Delta t^3)\right) - \left(x(t) + \dot{x}(t)\Delta t\right) $$
Упростим выражение:
$$ e_{\text{local}} = \frac{\ddot{x}(t)\Delta t^2}{2} + O(\Delta t^3) $$
Таким образом, локальная ошибка метода прямого Эйлера пропорциональна квадрату шага по времени:
$$ e_{\text{local}} = O(\Delta t^2) $$
Глобальная ошибка. Пусть $(T)$ – общее время интегрирования, тогда $(N = \frac{T}{\Delta t})$. Глобальная ошибка определяется как сумма локальных ошибок на каждом шаге:
$$ e_{\text{global}} = \sum_{k=0}^{N-1} e_{\text{local}, k} $$
Поскольку локальная ошибка на каждом шаге пропорциональна $(\Delta t^2)$, глобальная ошибка пропорциональна числу шагов умноженному на локальную ошибку:
$$ e_{\text{global}} = N \cdot O(\Delta t^2) = \frac{T}{\Delta t} \cdot O(\Delta t^2) = O(T \Delta t) $$
Таким образом, глобальная ошибка метода прямого Эйлера пропорциональна шагу по времени:
$$ e_{\text{global}} = O(\Delta t) $$
- Локальная ошибка метода прямого Эйлера пропорциональна квадрату шага по времени: $O(\Delta t^2)$.
- Глобальная ошибка метода прямого Эйлера пропорциональна шагу по времени: $O(\Delta t)$.
Получается что локальная ошибка метода Эйлера пропорциональна квадрату шага по времени. Глобальная ошибка же пропорциональна числу шагов по времени умноженному на локальную ошибку.
Анализ энергии
Использование в движках
Этот метод используется только на начальном этапе разработки движках. Вот, например, ребята предлагают поменять интегратор в годоте. Базовое правило – если можно не использовать этот метод – не используйте. Он простой как пробка, но супер неустойчивый и неточный. Да и какой в нем смысл, если он даже не может проинтегрировать простейшую пружинку.
Обратный метод Эйлера
Для прямого Эйлера мы взяли определение производной справа. Теперь попробуем взять его слева. $$ \begin{equation} \dot{x} = \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0} \frac{x(t) -x(t - \Delta t)}{\Delta t} \approx \frac{x(t) -x(t - \Delta t)}{\Delta t}, \end{equation} $$
$$ \begin{equation} x(t - \Delta t) = x(t) - \dot{x}(t)\Delta t \end{equation} $$ Или в дискретной форме $$ \begin{equation} x_{k-1} = x_k - \dot{x_k}\Delta t \end{equation} $$
Такие схемы называются неявными, т.к. зная $x_k$, нужно решить уравнение $f(x_{k-1}) = \dot{x_k}$ для нахождения $x_{k-1}$. Выглядит достаточно сложно, и такое просто не решить. В чистом виде такую схему никто не использует. Тк уравнение системы редко получаются линейными. Но мы сейчас анализируем линейную систему, поэтому можем попробовать просимулировать наши модельные задачи
Формальности
Решение задачи стрельбы из пушки с помощью обратного Эйлера $$ \dot{z} = A \cdot z + G $$ Подставляя это в метод обратного Эйлера получим $$ \begin{equation*} \begin{split} z_{k-1} = z_k - A\cdot z_k\cdot\Delta t - G\cdot\Delta t = \\ = (I - A\cdot\Delta t)\cdot z_k - G\cdot\Delta t \\ z_{k-1} = F\cdot z_k - G\cdot\Delta t \end{split} \end{equation*} $$
И выражая из последнего уравнения $z_k$ получим $$ z_{k} = F^{-1}\cdot(z_{k-1} + G\cdot\Delta t) $$
Почему в обратном методе Эйлера энергия убывает
Обратный метод Эйлера и убывание энергии
Рассмотрим уравнение гармонического осциллятора, описывающее движение пружины:
$$ \ddot{x} = -\frac{k}{m}x $$
Перепишем его в виде системы уравнений первого порядка:
$$ \begin{equation*} \begin{split} \dot{x} = v \ \dot{v} = -\frac{k}{m}x \end{equation*} \end{split} $$
Используя метод обратного Эйлера, получаем следующую дискретную форму:
$$ \begin{equation*} \begin{split} x_{k+1} = x_k + v_{k+1} \Delta t \ v_{k+1} = v_k - \frac{k}{m}x_{k+1} \Delta t \end{equation*} \end{split} $$
Подставим (x_{k+1}) во второе уравнение:
$$ v_{k+1} = v_k - \frac{k}{m}(x_k + v_{k+1} \Delta t) \Delta t $$
Решим относительно (v_{k+1}):
$$ v_{k+1} = \frac{v_k - \frac{k}{m} x_k \Delta t}{1 + \frac{k}{m} \Delta t^2} $$
Подставим это в первое уравнение для (x_{k+1}):
$$ x_{k+1} = x_k + \frac{v_k - \frac{k}{m} x_k \Delta t}{1 + \frac{k}{m} \Delta t^2} \Delta t $$
Теперь определим полную энергию системы, состоящую из кинетической и потенциальной энергии:
$$ E = \frac{1}{2}mv^2 + \frac{1}{2}kx^2 $$
Подставим выражения для (x_{k+1}) и (v_{k+1}) и посмотрим, как изменяется энергия:
$$ E_{k+1} = \frac{1}{2}m v_{k+1}^2 + \frac{1}{2}k x_{k+1}^2 $$
Рассчитаем энергию на шаге (k+1):
$$ E_{k+1} = \frac{1}{2}m \left( \frac{v_k - \frac{k}{m} x_k \Delta t}{1 + \frac{k}{m} \Delta t^2} \right)^2 + \frac{1}{2}k \left( x_k + \frac{v_k - \frac{k}{m} x_k \Delta t}{1 + \frac{k}{m} \Delta t^2} \Delta t \right)^2 $$
Упростим выражение:
$$ E_{k+1} = \frac{1}{2}m \left( \frac{v_k - \frac{k}{m} x_k \Delta t}{1 + \frac{k}{m} \Delta t^2} \right)^2 + \frac{1}{2}k \left( x_k + \frac{v_k \Delta t - \frac{k}{m} x_k \Delta t^2}{1 + \frac{k}{m} \Delta t^2} \right)^2 $$
Заметим, что ( \frac{1}{1 + \frac{k}{m} \Delta t^2} ) является коэффициентом, который уменьшает значения (v_{k+1}) и (x_{k+1}), что приводит к убыванию энергии:
$$ E_{k+1} < E_k $$
Таким образом, метод обратного Эйлера приводит к убыванию энергии в системе, что делает его устойчивым для задач, требующих сохранения или уменьшения энергии, таких как симуляция гармонических осцилляторов.
Метод обратного Эйлера, несмотря на свою сложность, лучше подходит для долгосрочных симуляций консервативных систем, поскольку приводит к убыванию энергии и, как следствие, к стабильному поведению системы.
Устойчивость
Да и вообще у неявного Эйлера очень большая зона устойчивости.
\input{pics/stable*zone_bwd.tex} Для неявного метода, переходя к собственным векторам, получим $$ \begin{equation} y_{k+1} = (1 - \Delta t \cdot \lambda)^{-1}\cdot y_k \end{equation} $$ Для устойчивости решения необходимо $$ \begin{equation} |(1 - \Delta t \cdot \lambda)^{-1}| < 1 \Leftrightarrow |1 - \Delta t \cdot \lambda| > 1 \end{equation} $$
Сразу можно заметить, что зона устойчивости для неявного метода больше
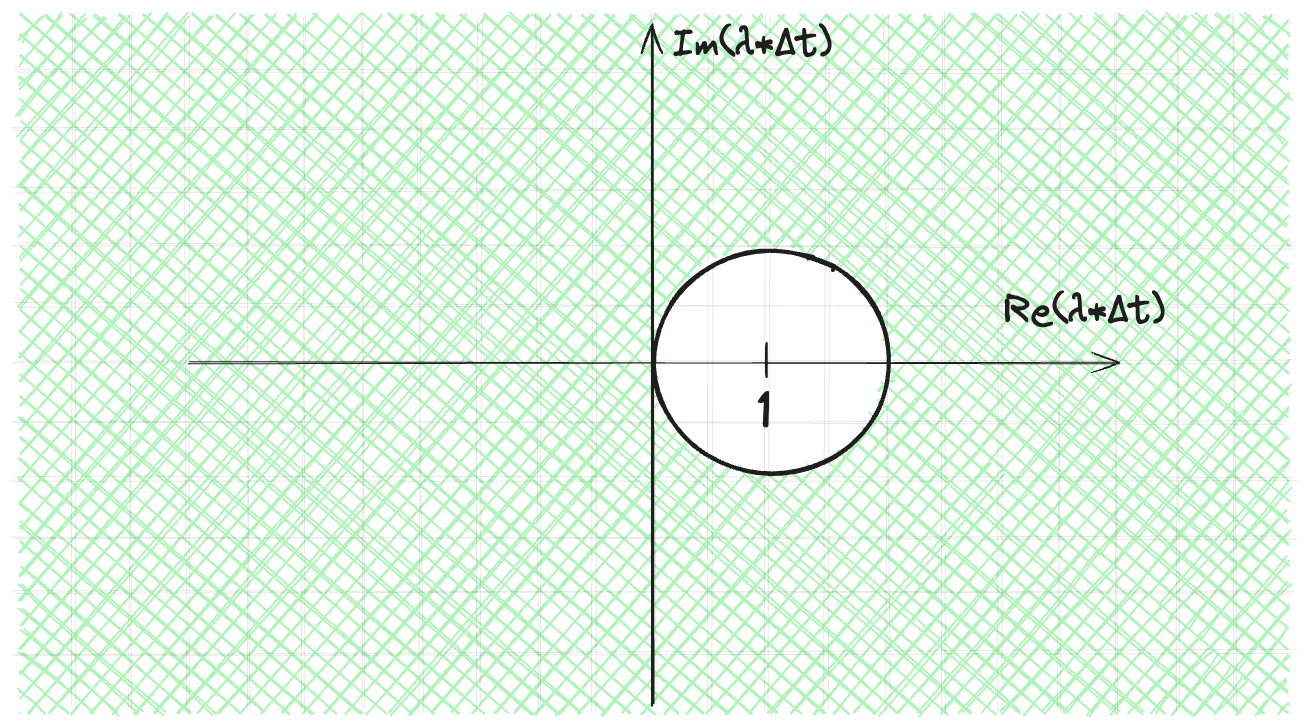
Подставляя на место $\dot{z}$ обсужденное выше приближенное значение, получим следующие равенствo для неявной$(2)$ схем: $$ \begin{equation} z_{k+1} = (I - A\cdot\Delta t)^{-1}\cdot z_k = B\cdot z_k\qquad (2) \end{equation} $$ По индукции, получим $$ \begin{equation} z_k = B^k\cdot z_0\qquad (2) \end{equation} $$
Точность
У обратного Эйлера точно такая же точность как и у прямого. локальная ошибка на каждом шаге пропорциональна квадрату шага по времени $\Delta t^2$, а глобальная ошибка пропорциональна $\Delta t$.
Использование в движках
Неявный метод очень сложно реализовать. Для симуляции простой пружинки, нам пришлось обратить матрицу, но если у нас более сложная система с ограничениями уравнение неявной схемы станет нелинейной. Поэтому их модифицируют дальше и например в XPBD, делают разложение по Тейлору до первого порядка. Такой метод используется в PhysX.
Или например в Projective Dynamics, используют упрощение оптимизационной задачи для решения уравнения.
Summary
С большой вероятностью вы не будете использовать эти методы. Слишком они простые и неустойчивые. Если вам нужно интегрировать уравнения движения с силами и другими сложными взаимодействиями, используйте методы из следующих глав. Умные люди придумали схемы получше)