2. Симплектические методы
Эти методы специально разработаны для решения задач, с которыми часто сталкиваются в физике игр. Если с помощью прямого и обратного метода Эйлера можно решить любой дифур первого порядка, то симплектические методы работают в физике игр работают только для систем вида $$ \begin{equation} \begin{split} &\dot{v} = f(x) \\ &\dot{x} = g(v) \end{split} \end{equation} $$
Если погуглить, википедия
<p>symplectic integrator (SI) is a numerical integration scheme for Hamiltonian systems. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations $\dots$ The time evolution of Hamilton’s equations is a symplectomorphism, meaning that it conserves the symplectic 2-form $dp \times dq$. A numerical scheme is a symplectic integrator if it also conserves this 2-form.</p>
Я не знаю до конца в каком порядке все происходило но составил примерно такую картину. Есть теорема Лиувиля которая говорит следующее:
<p>Функция распределения гамильтоновой системы постоянна вдоль любой траектории в фазовом пространстве.</p>
Сама формулировка мало что говорит, но ее геометрическая интерпретация говорит о том, что объемы в фазовом пространстве сохраняются.
Все еще мало что понятно, но для нас простых пользователей нужно знать следующее В гамильтоновых системах энергия сохраняется и в таких системах объемы в фазовом пространстве сохраняются.
Т. е если взять несколько точек в фазовом пространстве, и посмотреть как они двигаются, то они будут двигаться так, что объемы будут сохраняться. Вот здесь например 4 точки с разными начальными условиями в системе с пружинкой и они двигаются по фазовым траекториям. Мы как будто следим одновременно за 4 пружинками и рисуем их графики.
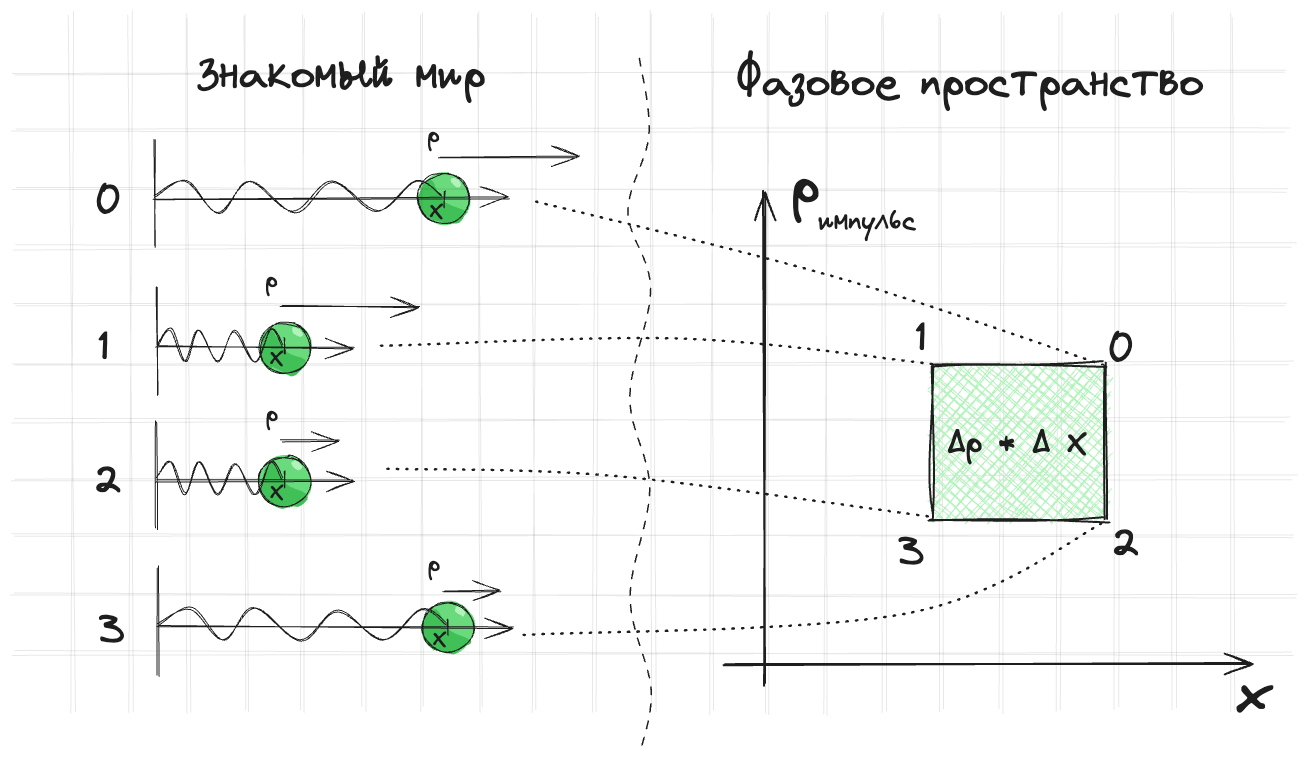
А двигаться такая система будет вот так:
И если мы посмотрим на объем который они занимают, то он будет сохраняться. Об этом и говорит теорема Лиувиля (ну она говорит гораздо больше и умнее, но нам нужно только вот этот момент).
Так вот идея симплектических методов повторить следствие теоремы Лиувиля в численном методе. Если энергия сохраняется, то и объемы в фазовом пространстве сохраняются. И если мы будем использовать методы, которые сохраняют объемы, то мы лучше будем сохранять энергию. Хочу очень сильно подчеркнуть, что симплектические методы не сохраняют аналитическую энергию, Они сохраняют что-то похожее на нее. И это не всегда работает, но в большинстве случаев это лучше чем ничего. Существуют методы которые способны полностью сохранять энергию, не всегда применимы на практике или дают странные результаты.
Почему так: базовая идея – сохранение фазового объема – задача которая ограничивает траекторию решения сильнее чем сохранение энергии и как следствие методы которые сохраняют фазовый объем работают лучше и ближе к аналитическому решению. Есть статья в которой говорится, что нельзя создать численный метод который бы для любой системы сохранял энергию и фазовый объем, поэтому нам остается пользоваться тем что есть.
Давайте для примера посмотрим что происходит с фазовым объемом для явного и неявного метода в пружинке
Ну в принципе достаточно ожидаемые результаты. У явного метода росла энергия и здесь видно что и объем растет. У неявного наоборот все уменьшается.
Symplectic Euler
У этого метода очень много названий – Semi-implicit Euler, Semi-explicit Euler, Symplectic Euler, Störmer-Verlet method. Самый простой и самый популярный симплектический метод – это метод полуявного Эйлера.
Его идея используется во многих физических движках. Базовая идея такая: У нас уравнение движения второго порядка. Сначала нужно интегрировать ускорение и получать скорость, потом скорость и получать позицию. Раньше мы решали это одновременно явным или неявным методом. А какие свойства мы получим если одно уравнение будем решать явно, а другое неявно?
Наиболее популярная вариация этого метода – это метод полуявного Эйлера. $$ \begin{equation} \begin{split} &v_{k+1} = v_k + f(x_k, v_{k+1})\Delta t \\ &x_{k+1} = x_k + g(x_k, v_{k+1}) \end{split} \end{equation} $$
Собственно он полуявный (полунеявный) тк в общем виде численная схема для расчета скорости неявная, а схема координаты явная. Для того чтобы не иметь дело с неявным методом обычно полуявный метод рассматривают для систем в котором скорость зависит только от координаты. Т.е. $f(x, v) = f(x)$. На самом деле это не совсем так, тк простой демпинг вида $d(v) = -dv $ Делает уравнение пружинки видом $f(x, v) = kx + d*v$. Но эту проблему решают по-разному.
Обычно считают что $g(x, v) = v$. Т.е позиция зависит только от скорости.
Тогда итоговая система выглядит так: $$ \begin{equation} \begin{split} &\dot{v} = f(x) + g(v) \\ &\dot{x} = v \end{split} \end{equation} $$ И для такой системы очень удобно использовать полуявный метод Эйлера.
$$ \begin{equation} \begin{split} &v_{k+1} = v_k + f(x_k)\Delta t \\ &x_{k+1} = x_k + v_{k+1}\Delta t \end{split} \end{equation} $$
Мы получаем очень простое выражение для скорости на следующем шаге и для позиций.
Давайте на примерах. Вот что будет если просимулировать пружинку с помощью полуявного метода.
Вот еще пример того что сохранения фазового объема не сохраняет энергию.
Поскольку координата и скорость постоянно меняются, то для того чтобы показавать фазовое пространство я отцентрировал его в середине аналитического решения.
Объем сохраняется, но энергия падает тк появляется ошибка в скорости и позиции которые накапливаются со временем. Тк решение не периодическое у нас нет шанса сбалансировать ошибку.
Анализ устойчивости
Если с прямым и обратным Эйлером все было понятно: есть уравнение системы, считаем его собственные значения и смотрим удовлетворяет ли они условиям устойчивости. То с симплектическими методами все немного сложнее. Если в общем случае, то устойчивость симплектических методов определяется устойчивостью каждого уравнения системы.
Для нас, как для создателей новых физических движков интересен следующий факт, что всякие осцилирующие или периодические системы условно устойчивы. Те мы можем подобрать такой шаг по времени, что решение не развалится.
Должно выполняться условие $(\Delta t * w) < 2$ где $w$ – частота осцилляции. Если мы хотим визуализировать такие осциляции мы в любом случае должны требовать чтобы $\Delta t « w$. Тк иначе мы просто не увидим этих колебаний.
Анализ точности
У полуявного Эйлера локальный второй порядок точности как и у обычного Эйлера. И в общем случае первый порядок глобальной точности. Но для периодических систем работает симплектическая магия и ошибка не накапливается.
Использование в движках
Если нужно симулировать твердые тела – это очень хороший метод. Он используется в Box2D, Jolt, Godot, Bullet, ODE. Про другие не знаю. Очень дешевый по количеству вычислений, достаточно стабильный и хорошо работает с ограничениями и коллизиями твердых тел.
Классический Метод Верле
Также известен как Verlet integration, Störmer’s method. Идея такая: Если разложить в ряд Тейлора $x_{k+1}$ и $x_{k-1}$ $$ \begin{equation} \begin{split} &x_{k+1} = x_k + v_k\Delta t + \frac{1}{2}a_k\Delta t^2 + \frac{1}{6}b_k\Delta t^3 + O(\Delta t^4) \\ &x_{k-1} = x_k - v_k\Delta t + \frac{1}{2}a_k\Delta t^2 + \frac{1}{6}b_k\Delta t^3 + O(\Delta t^4) \end{split} \end{equation} $$
Сложить эти два уравнения и выразить $x_{k+1}$: $$ \begin{equation} x_{k+1} = 2x_k - x_{k-1} + a_k\Delta t^2 + O(\Delta t^4) \end{equation} $$ Это класическое представление метода Верле. В этом выражении нет скорости и если она вам не нужна, то это самый простой метод. Но часто для обработки коллизий в физическом движке нужна скорость в явном виде. Некоторые просто берут скорость из предыдущего шага, и для определенных целей это работает. Но например для Sequential Impulse метода это не подходит. Проблема здесь следующая – если вам все-таки нужны скорости, например для обработки коллизии – вы их не получите. Ну точнее они будут бесполезны. При обработки коллизий удобно считать, что удар упругий и для этого нужно в явном виде изменить скорость и проинтегрировать позицию. Есть методы, которые позволяют избежать, но они подходят для симуляции материальных точек.
Точность
Четвертый порядок точности. Это очень хорошо.
Устойчивость
Velocity Verlet
Это модификация метода Верле, которая позволяет получить скорость в явном виде.
Вот так выглядит более популярная модификация метода, которая позволяет получить скорость в явном виде. Здесь мы считаем что тело движется равноускоренно на момент времени $\Delta t$. Это достаточно сильно усложняет интегрирование вращения, но для простых систем такой метод работает хорошо.